4 The Laplace Transform
4.1 Definition of the Laplace Transform
If \(f\) be a function defined for \(t \geq 0\), \(~\)then the integral
\[\mathcal{L}\{f(t)\} =\int_0^\infty f(t) e^{-st}\, dt =F(s)\]
is the Laplace Transform of \(~f\) provided the integral converges. The result is a function of \(s\)
\(~\)
Example \(\,\) Evaluate \(\mathcal{L}\{1\}\), \(~\mathcal{L}\{t\}\), \(~\)and \(~\mathcal{L}\{e^{-3t}\}\)
\(~\)
Example \(\,\) Evaluate \(\mathcal{L}\{f(t)\}~\) for \(~\displaystyle f(t) = \left\{\begin{matrix} 0, & 0 \leq t < 3\\ 2, & \phantom{0 \leq }\; t \geq 3 \end{matrix}\right.\)
\(~\)
\(\mathcal{L}\) is a linear transform
\[\mathcal{L}\{\alpha f(t) +\beta g(t)\} = \alpha \mathcal{L} \{f(t)\} +\beta\mathcal{L}\{g(t)\} =\alpha F(s) +\beta G(s)\]
\(~\)
Example \(\,\) Find \(\mathcal{L}\{f(t)\}\) by first using an appropriate trigonometric identity \(~f(t)=\sin^2 2t\)
\(~\)
Example \(\,\) Find \(\mathcal{L}\{f(t)\}\)
\(~f(t)=\left\{\begin{matrix} -1, & 0 \leq t < 1\\ \phantom{-}1, & t \geq 1\quad\;\; \end{matrix}\right.\)
\(~f(t)=\left\{\begin{matrix} \phantom{-}t, & 0 \leq t < 1\\ \phantom{-}1, & t \geq 1\quad\;\; \end{matrix}\right.\)
\(~f(t)=\left\{\begin{matrix} \sin t,& 0 \leq t < \pi\\ 0,& t \geq \pi \quad\;\; \end{matrix}\right.\)
\(~\)
Example \(\,\) Find \(\mathcal{L}\{f(t)\}\)
\(~f(t)=e^{t+7}\)
\(~f(t)=e^t \cos t\)
\(~f(t)=t\cos t\)
\(~f(t)=\sin 3t \cos 3t\)
\(~f(t)=\sin^4 t\)
\(~\)
4.2 The Inverse Transform and Transforms of Derivatives
If \(F(s)\) represents the Laplace transform of \(~f(t)\), \(~\)then \(f(t)\) is the inverse Laplace transform of \(F(s)\)
\[f(t)=\mathcal{L}^{-1}\{F(s)\}\]
\(\mathcal{L}^{-1}\) is a linear transform
\[\mathcal{L}^{-1}\{\alpha F(s) +\beta G(s)\} = \alpha \mathcal{L}^{-1} \{F(s)\} +\beta\mathcal{L}^{-1}\{G(s)\} =\alpha f(t) +\beta g(t)\]
\(~\)
Example \(\,\) Find the given inverse transform
\(\displaystyle \mathcal{L}^{-1} \left\{ \frac{1}{s^3} \right\}\)
\(~\)
\(\displaystyle \mathcal{L}^{-1} \left\{ \frac{1}{s^2} - \frac{48}{s^5} \right\}\)
\(~\)
\(\displaystyle \mathcal{L}^{-1} \left\{ \frac{(s+1)^3}{s^4} \right\}\)
\(\displaystyle \mathcal{L}^{-1} \left\{ \frac{1}{4s^2+1} \right\}\)
\(~\)
\(\displaystyle \mathcal{L}^{-1} \left\{ \frac{s+1}{s^2+2} \right\}\)
\(~\)
Example \(\,\) Evaluate \(\displaystyle\mathcal{L}^{-1}\left\{\frac{-2s +6}{s^2 +4}\right\}\)
\(~\)
Transforms of derivatives
\[ \begin{aligned} \mathcal{L}\{f'(t)\} &= sF(s) -f(0)\\ \mathcal{L}\{f''(t)\} &= s^2F(s) -sf(0) -f'(0)\\ &\; \vdots \end{aligned}\]
\(\displaystyle\mathcal{L}\left\{\frac{d^n f}{dt^n}\right\}\) depends on \(F(s)=\mathcal{L}\{f(t)\}\) and the \(n-1\) derivatives of \(~f(t)\) evaluated at \(t=0\)
If \(~f\) is piecewise continuous on \([0, \infty]\) and of exponential order, then
\[\lim_{s \to \infty} \mathcal{L}\{f(t)\}=0\]
The Laplace transform of a linear DE with constant coefficients becomes an algebraic equation in \(Y(s)\)
\(~\)
Example \(\,\) Use the Laplace transform to solve the IVP
\[\frac{dy}{dt} +3y = 13\sin 2t, \;y(0)=6\]
\(~\)
Example \(\,\) Use the Laplace transform to solve the given initial-value problem
\(~y''+y=\sqrt{2} \sin \sqrt{2}t, \;\;y(0)=10,\;y'(0)=0\)
\(~2y'''+3y''-3y'-2y=e^{-t}, \;\;y(0)=0, \;y'(0)=0, \; y''(0)=1\)
\(~\)
4.3 Translation Theorems
First Translation Theorem
If \(\mathcal{L}\{f(t)\}=F(s)~\) and \(~a\) is any real number, \(~\)then
\[\mathcal{L}\{e^{-at}f(t)\}=F(s+a)\]
\(~\)
Example \(\,\) Evaluate \(\mathcal{L}\{e^{-2t}\cos 4t\}\) and \(\displaystyle\mathcal{L}^{-1}\left\{\frac{2s +5}{(s +3)^2}\right\}\)
\(~\)
Second Translation Theorem
If \(\mathcal{L}\{f(t)\}=F(s)~\) and \(~a >0\), then
\[\mathcal{L}\{f(t -a)\mathcal{U}(t -a)\}=e^{-as}F(s)\]
Alternative Form
\[ \begin{aligned} \mathcal{L}\{g(t)\mathcal{U}(t -a)\} &= {\small\int_a^\infty e^{-st} g(t)\,dt}\\ &={\small \int_0^\infty e^{-s(t'+a)} g(t' +a) \,dt'} \\&= e^{-as} \mathcal{L}\{g(t+a)\} \end{aligned}\]
\(~\)
Example \(\,\) Find either \(~F(s)\) or \(~f(t)\)
\(\mathcal{L}\{ te^{10t} \}\)
\(\mathcal{L}\{ t^{10}e^{-7t}\}\)
\(\mathcal{L}\{ e^t \sin 3t \}\)
\(\displaystyle \mathcal{L}^{-1} \left\{ \frac{s}{(s+1)^2} \right\}\)
\(\displaystyle \mathcal{L}^{-1} \left\{ \frac{2s-1}{s^2(s+1)^3} \right\}\)
\(~\)
Example \(\,\) Solve \(~y' +y = f(t)\), \(~\)\(y(0)=5\), where
\[f(t) = \begin{cases} 0, & 0 \leq t < \pi\\ 3\cos t ,& t \geq \pi \end{cases}\]
\(~\)
4.4 Additional Operational Properties
Derivatives of Transforms: \(~\) If \(F(s)=\mathcal{L}\{f(t)\}~\) and \(n=1,2,\cdots,\) then
\[\mathcal{L}\{t^nf(t)\}=(-1)^n \frac{d^n}{ds^n} F(s)\]
\(~\)
Convolution Theorem: \(\,\) \(\displaystyle f*g=\int_0^t f(\tau)g(t -\tau)\, d\tau\)
\[\mathcal{L}\{f*g\}=\mathcal{L}\{f(t)\} \mathcal{L}\{g(t)\} =F(s) G(s)\]
\(~\)
Transform of a Periodic Function: \(~\) \(f(t+T)=f(t)\)
\[\mathcal{L}\{f(t)\}=\frac{1}{1-e^{-sT}} \int_0^T e^{-st} f(t) \,dt\]
\(~\)
Example \(\,\) Evaluate \(~\mathcal{L}\{t\sin \omega t\}\)
\(~\)
Example \(\,\) Solve \(~x'' +16x =\cos 4t, \; x(0)=1, \; x'(0)=1\)
\(~\)
Example \(\,\) Evaluate \(\displaystyle\mathcal{L}^{-1}\left\{\frac{1}{(s^2 +\omega^2)^2}\right\}\)
\(~\)
Example \(\,\) Evaluate \(\displaystyle\mathcal{L} \left\{ \int_0^t f(\tau)\, d\tau \right\}\)
\(~\)
Example \(\,\) Solve \(\displaystyle \,f(t) =3t^2 -e^{-t} -\int_0^t f(\tau)\, e^{t -\tau}\, d\tau\;\) for \(f(t)\)
\(~\)
Example \(\,\) Find the Laplace transform of the periodic function
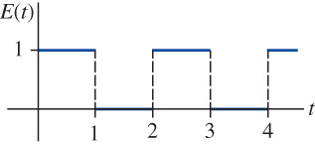
\[\scriptsize\mathcal{L}\{E(t)\}=\frac{1}{1 -e^{-2s}} \int_0^2 e^{-st} E(t)\,dt=\frac{1}{s(1 +e^{-s})}\]
\(~\)
Example \(\,\) Evaluate the given Laplace transform
\(~\mathcal{L}\left\{ te^{-10t} \right\}\)
\(~\mathcal{L}\left\{ t\cos 2t \right\}\)
\(~\mathcal{L}\left\{ te^{2t}\sin 6t \right\}\)
\(~\)
Example \(\,\) Use the Laplace transform to solve the given initial-value problem
\(~y'+y=t \sin t, \;y(0)=0\)
\(~y''+9y=\cos 3t, \;y(0)=2, \;y'(0)=5\)
\(~\)
Example \(\,\) Find the convolution \(~f*g\) of the given functions. After integrating find the Laplace transform \(~f*g\)
\(~f(t)=4t, \;g(t)=3t^2\)
\(~f(t)=e^{-t}, \;g(t)=e^t\)
\(~\)
Example \(\,\) Find the Laplace transform
- \(~\mathcal{L} \left\{ e^{-t}* e^t \cos t \right\}\)
\(~\)
Example \(\,\) Evaluate the given inverse transform
- \(~\displaystyle \mathcal{L}^{-1} \left\{ \frac{1}{s^3(s-1)} \right\}\)
\(~\)
Example \(\,\) Use the Laplace transform to solve the given integral or integrodifferential equation
\(~\displaystyle f(t) +2\int_0^t f(\tau)\cos (t-\tau)\,d\tau=4e^{-t}+\sin t\)
\(~\displaystyle \frac{dy}{dt}=10-\int_0^t e^{-4\tau} y(t-\tau)\,d\tau, \;y(0)=5\)
\(~\)
Example \(\,\) The Laplace transform \(\mathcal{L} \left\{ e^{-t^2} \right\}\) exists, but without finding it solve the initial-value problem
- \(~y''+9y=3e^{-t^2}, \;\;y(0)=0, \;y'(0)=0\)
\(~\)
Example \(\,\) Solve the integral equation
- \(~\displaystyle f(t)=e^t+e^t \int_0^t e^{-\tau} f(\tau)\, d\tau\)
\(~\)
4.5 The Dirac Delta Function
\[\textbf{Unit Pulse}\]
\[\small \delta_a(t-t_0) = \left\{\begin{matrix} 0, & \;\;\;\;\;\;\; 0 \leq t < t_0 -a\\ \frac{1}{2a}, & t_0 -a \leq t \leq t_0 +a\\ 0, & \;\; t \geq t_0 +a \end{matrix}\right.\]
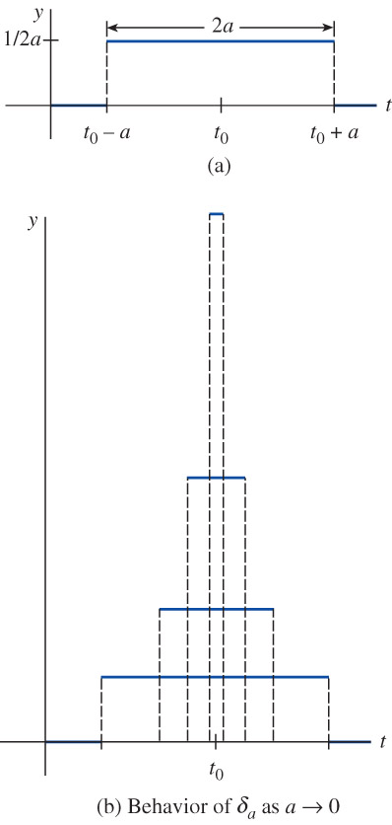
The Dirac Delta Function
\[ \begin{aligned} \delta(t -t_0) &= \lim_{a \to 0} \,\delta_a(t -t_0) \\ &\Downarrow \\ \mathcal{L}\{\delta(t -t_0)\} &= \lim_{a \to 0} \mathcal{L}\{\delta_a(t -t_0)\}=e^{-st_0}\lim_{a \to 0} \left(\frac{e^{sa} -e^{-sa}}{2sa}\right)\\ &= e^{-st_0} \end{aligned}\]
When \(~t_0=0\), \(~\)\(\displaystyle\mathcal{L}\{\delta(t)\}=1\)
\(~\)
Example \(\,\) Solve \(~y'' +y=4\delta(t -2\pi)\) \(~\)subject to \(y(0)=1, \;y'(0)=0\)
\(~\)
Example \(\,\) Use the Laplace transform to solve the given differential equation subject to the indicated initial conditions
\(~y'-3y=\delta(t-2), \;y(0)=0\)
\(~y''+y=\delta(t-2\pi), \;y(0)=0, \,y'(0)=1\)
\(~y''+y=\delta(t-\pi/2)+\delta(t-3\pi/2),\;y(0)=0,\,y'(0)=0\)
\(~\)
4.6 Systems of Linear Differential Equations
- When initial conditions are specified, \(~\)the Laplace transform reduces a system of linear DEs to a set of simultaneous algebraic equations in the transformed functions
\(~\)
Example \(\,\) Double Pendulum
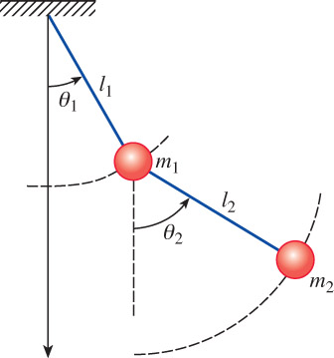
Linearization \(\,\) For small displacements \(\theta_1\) and \(\theta_2\),
\[ \begin{aligned} (m_1 +m_2) l_1 \ddot{\theta_1} +m_2 l_2 \ddot{\theta_2} +(m_1 +m_2) g \,\theta_1 &= 0\\ l_2 \ddot{\theta_2} +l_1 \ddot{\theta_1} +g \,\theta_2 &= 0 \end{aligned}\]
Solve the system when
\[m_1=3, m_2=1, l_1=l_2=5, \text{ and } ~g=10\]
\[\theta_1(0) = 1, \theta_2(0)=-1, \dot{\theta_1}(0)=0, \dot{\theta_2}(0)=0\]
\(~\)
Example \(\,\) Use the Laplace transform to solve the given system of differential equations
\[ \begin{aligned} \dot{x} &= -x+y \\ \dot{y} &= 2x, \;\;x(0)=0,\;y(0)=1 \end{aligned}\]
\[ \begin{aligned} \dot{x} &= x-2y \\ \dot{y} &= 5x-y, \;\;x(0)=-1,\;y(0)=2 \end{aligned}\]
\[ \begin{aligned} 2&\dot{x}+\dot{y} -2x= 1 \\ &\dot{x}+\dot{y} -3x -3y= 2, \;\;x(0)=0,\;y(0)=0 \end{aligned}\]