Appendix A — Numpy: Vectors, Matrices, and Multidimensional Arrays

\(~\)

\(~\)

A.1 Importing numpy

import numpy as np

print("numpy: ", np.__version__)
numpy:  2.3.1

A.2 The Numpy array object

data = np.array([[1, 2], [3, 4], [5, 6]])
data
array([[1, 2],
       [3, 4],
       [5, 6]])
type(data)
numpy.ndarray
data.ndim
2
data.shape
(3, 2)
data.size
6
data.dtype
dtype('int64')
data.nbytes
48

A.3 Data types

d0 = np.array([1, 2, 3], dtype=int)
d0
array([1, 2, 3])
d1 = np.array([1, 2, 3], dtype=float)
d1
array([1., 2., 3.])
d2 = np.array([1, 2, 3], dtype=complex)
d2
array([1.+0.j, 2.+0.j, 3.+0.j])

A.3.1 Type casting

data = np.array([1, 2, 3], dtype=float)
data
array([1., 2., 3.])
data = np.array(data, dtype=int)
data
array([1, 2, 3])
data = np.array([1.6, 2, 3], dtype=float)
data.astype(int)
array([1, 2, 3])

A.3.2 Type promotion

d1 = np.array([1, 2, 3], dtype=float)
d2 = np.array([1, 2, 3], dtype=complex)
d1 + d2
array([2.+0.j, 4.+0.j, 6.+0.j])
(d1 + d2).dtype
dtype('complex128')

A.3.3 Type-depending operation

np.sqrt(np.array([-1, 0, 1]))
/var/folders/4x/8kn2nym12cn7x7qmg_6s4b8h0000gn/T/ipykernel_76845/208196152.py:1: RuntimeWarning: invalid value encountered in sqrt
  np.sqrt(np.array([-1, 0, 1]))
array([nan,  0.,  1.])
np.sqrt(np.array([-1, 0, 1], dtype=complex))
array([0.+1.j, 0.+0.j, 1.+0.j])

A.3.4 Real and imaginary parts

data = np.array([1, 2, 3], dtype=complex)
data
array([1.+0.j, 2.+0.j, 3.+0.j])
data.real
array([1., 2., 3.])
data.imag
array([0., 0., 0.])
np.real(data)
array([1., 2., 3.])
np.imag(data)
array([0., 0., 0.])

A.3.5 Order of array data in memory

  • Multidimensional arrays are stored as contiguous data in memory. \(~\)Consider the case of a two-dimensional array, \(~\)containing rows and columns: \(~\)One possible way to store this array as a consecutive sequence of values is to store the rows after each other, and another equally valid approach is to store the columns one after another

  • The former is called row-major format and the latter is column-major format. Whether to use row-major or column-major is a matter of conventions, and the row-major format is used for example in the C programming language, and Fortran uses the column-major format

  • A numpy array can be specified to be stored in row-major format, using the keyword argument order='C', and column-major format, using the keyword argument order='F', when the array is created or reshaped. The default format is row-major

  • In general, the numpy array attribute ndarray.strides defines exactly how this mapping is done. The strides attribute is a tuple of the same length as the number of axes (dimensions) of the array. Each value in strides is the factor by which the index for the corresponding axis is multiplied when calculating the memory offset (in bytes) for a given index expression

data = np.array([[1, 2, 3], [4, 5, 6]], dtype=np.int32)
data
array([[1, 2, 3],
       [4, 5, 6]], dtype=int32)
data.strides
(12, 4)
data = np.array([[1, 2, 3], [4, 5, 6]], dtype=np.int32, order='F')
data
array([[1, 2, 3],
       [4, 5, 6]], dtype=int32)
data.strides
(4, 8)

A.4 Creating arrays

A.4.1 Arrays created from lists and other array-like objects

data = np.array([1, 2, 3, 4])
data.ndim, data.shape
(1, (4,))
data = np.array(((1, 2), (3, 4)))
data.ndim, data.shape
(2, (2, 2))

A.4.2 Arrays filled with constant values

np.zeros((2, 3))
array([[0., 0., 0.],
       [0., 0., 0.]])
data = np.ones(4)
data, data.dtype
(array([1., 1., 1., 1.]), dtype('float64'))
5.4 * np.ones(10)
array([5.4, 5.4, 5.4, 5.4, 5.4, 5.4, 5.4, 5.4, 5.4, 5.4])
np.full(10, 5.4) # slightly more efficient
array([5.4, 5.4, 5.4, 5.4, 5.4, 5.4, 5.4, 5.4, 5.4, 5.4])
x1 = np.empty(5)
x1.fill(3.0)
x1
array([3., 3., 3., 3., 3.])

A.4.3 Arrays filled with incremental sequences

np.arange(0, 11, 1)
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10])
np.linspace(0, 10, 11)  # generally recommended
array([ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.])

A.4.4 Arrays filled with logarithmic sequences

np.logspace(0, 2, 10)  # 5 data points between 10**0=1 to 10**2=100
array([  1.        ,   1.66810054,   2.7825594 ,   4.64158883,
         7.74263683,  12.91549665,  21.5443469 ,  35.93813664,
        59.94842503, 100.        ])

A.4.5 Mesh grid arrays

x = np.array([-1, 0, 1])
y = np.array([-2, 0, 2])

X, Y = np.meshgrid(x, y)
X
array([[-1,  0,  1],
       [-1,  0,  1],
       [-1,  0,  1]])
Y
array([[-2, -2, -2],
       [ 0,  0,  0],
       [ 2,  2,  2]])
Z = (X + Y)**2
Z
array([[9, 4, 1],
       [1, 0, 1],
       [1, 4, 9]])

A.4.6 Creating uninitialized arrays

np.empty(3, dtype=float)
array([0., 0., 0.])

A.4.7 Creating arrays with properties of other arrays

def f(x):    
    y = np.ones_like(x)    # compute with x and y    
    return y

x = np.array([[1, 2, 3], [4, 5, 6]])
y = f(x)
y
array([[1, 1, 1],
       [1, 1, 1]])

A.4.8 Creating matrix arrays

np.identity(4)
array([[1., 0., 0., 0.],
       [0., 1., 0., 0.],
       [0., 0., 1., 0.],
       [0., 0., 0., 1.]])
np.eye(4, k=1)
array([[0., 1., 0., 0.],
       [0., 0., 1., 0.],
       [0., 0., 0., 1.],
       [0., 0., 0., 0.]])
np.eye(4, k=-1)
array([[0., 0., 0., 0.],
       [1., 0., 0., 0.],
       [0., 1., 0., 0.],
       [0., 0., 1., 0.]])
np.diag(np.arange(0, 20, 5))
array([[ 0,  0,  0,  0],
       [ 0,  5,  0,  0],
       [ 0,  0, 10,  0],
       [ 0,  0,  0, 15]])

A.5 Indexing and slicing

A.5.1 One-dimensional arrays

a = np.arange(0, 11)
a
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10])
a[0]
np.int64(0)
a[-1]
np.int64(10)
a[4]
np.int64(4)
a[1:-1]
array([1, 2, 3, 4, 5, 6, 7, 8, 9])
a[1:-1:2]
array([1, 3, 5, 7, 9])
a[:5]
array([0, 1, 2, 3, 4])
a[-5:]
array([ 6,  7,  8,  9, 10])
a[::-2]
array([10,  8,  6,  4,  2,  0])

A.5.2 Multidimensional arrays

f = lambda m, n: n + 10*m
# please search for numpy.fromfunction at google
A = np.fromfunction(f, (6, 6), dtype=int)
A  
array([[ 0,  1,  2,  3,  4,  5],
       [10, 11, 12, 13, 14, 15],
       [20, 21, 22, 23, 24, 25],
       [30, 31, 32, 33, 34, 35],
       [40, 41, 42, 43, 44, 45],
       [50, 51, 52, 53, 54, 55]])
A[:, 1]  # the second column
array([ 1, 11, 21, 31, 41, 51])
A[1, :]  # the second row
array([10, 11, 12, 13, 14, 15])
A[:3, :3]
array([[ 0,  1,  2],
       [10, 11, 12],
       [20, 21, 22]])
A[3:, :3]
array([[30, 31, 32],
       [40, 41, 42],
       [50, 51, 52]])
A[::2, ::2]
array([[ 0,  2,  4],
       [20, 22, 24],
       [40, 42, 44]])
A[1::2, 1::3]
array([[11, 14],
       [31, 34],
       [51, 54]])

A.5.3 Views

  • Subarrays that are extracted from arrays using slice operations are alternative views of the same underlying array data. That is, \(~\)they are arrays that refer to the same data in memory as the original array, \(~\)but with a different strides configuration

  • When elements in a view are assigned new values, \(~\)the values of the original array are therefore also updated. For example,

B = A[1:5, 1:5]
B
array([[11, 12, 13, 14],
       [21, 22, 23, 24],
       [31, 32, 33, 34],
       [41, 42, 43, 44]])
B[:, :] = 0
A
array([[ 0,  1,  2,  3,  4,  5],
       [10,  0,  0,  0,  0, 15],
       [20,  0,  0,  0,  0, 25],
       [30,  0,  0,  0,  0, 35],
       [40,  0,  0,  0,  0, 45],
       [50, 51, 52, 53, 54, 55]])
  • When a copy rather than a view is needed, the view can be copied explicitly by using the copy method of the ndarray instance
C = B[1:3, 1:3].copy()
C
array([[0, 0],
       [0, 0]])
C[:, :] = 1
C
array([[1, 1],
       [1, 1]])
B
array([[0, 0, 0, 0],
       [0, 0, 0, 0],
       [0, 0, 0, 0],
       [0, 0, 0, 0]])

A.5.4 Fancy indexing and boolean-valued indexing

A = np.linspace(0, 1, 11)
A
array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ])
A[np.array([0, 2, 4])]
array([0. , 0.2, 0.4])
A[[0, 2, 4]]
array([0. , 0.2, 0.4])
A > 0.5
array([False, False, False, False, False, False,  True,  True,  True,
        True,  True])
A[A > 0.5]
array([0.6, 0.7, 0.8, 0.9, 1. ])
  • Unlike arrays created by using slices, \(~\)the arrays returned using fancy indexing and Boolean-valued indexing are not views, \(~\)but rather new independent arrays
A = np.arange(10)
indices = [2, 4, 6]
B = A[indices]
B[0] = -1
A
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
A[indices] = -1
A
array([ 0,  1, -1,  3, -1,  5, -1,  7,  8,  9])
A = np.arange(10)
B = A[A > 5]
B[0] = -1
A
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
A[A > 5] = -1
A
array([ 0,  1,  2,  3,  4,  5, -1, -1, -1, -1])

A.5.5 Summery

show_array((4, 4), ':, :')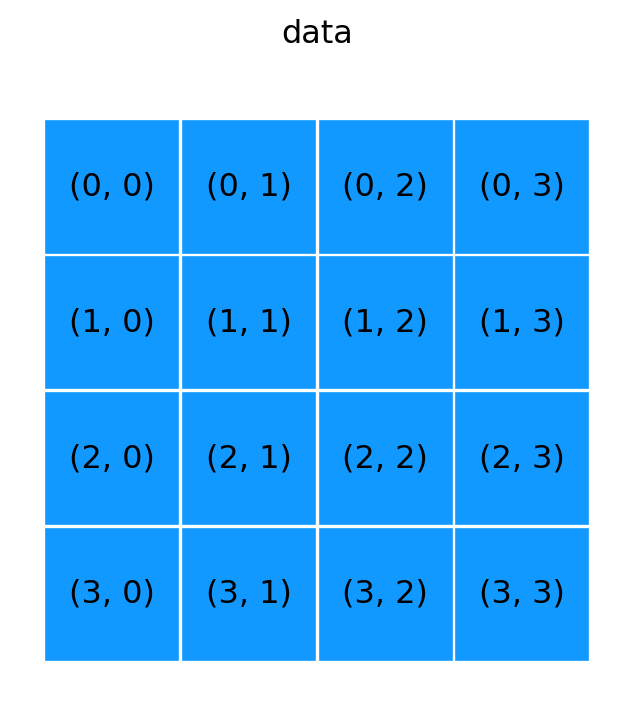

show_array((4, 4), '0')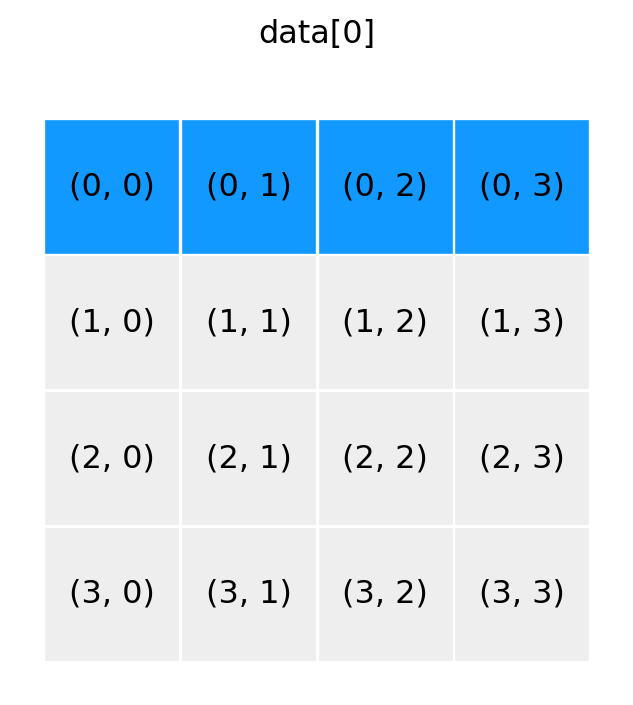

show_array((4, 4), '1, :')

show_array((4, 4), ':, 2')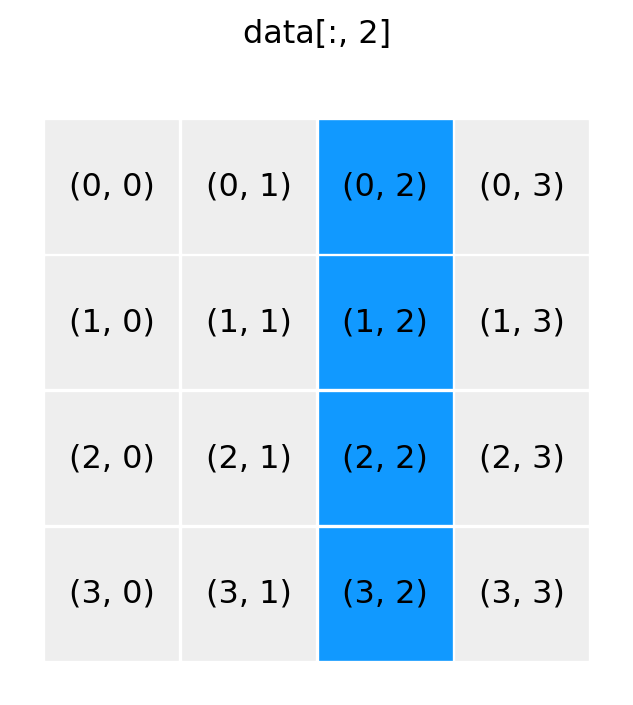

show_array((4, 4), '0:2, 0:2')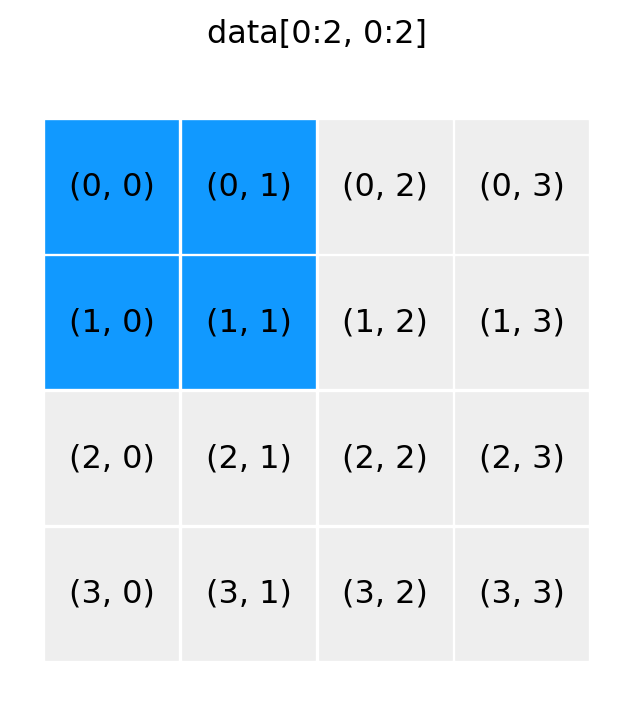

show_array((4, 4), '0:2, 2:4')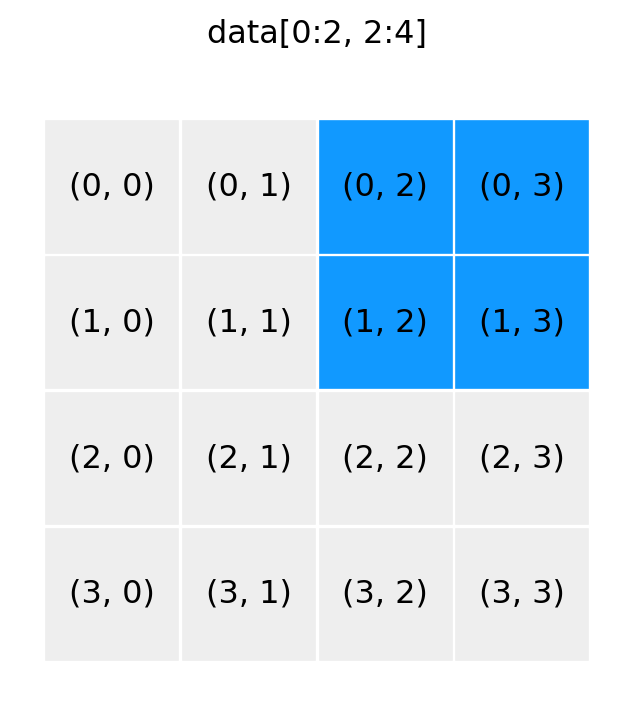

show_array((4, 4), '::2, ::2')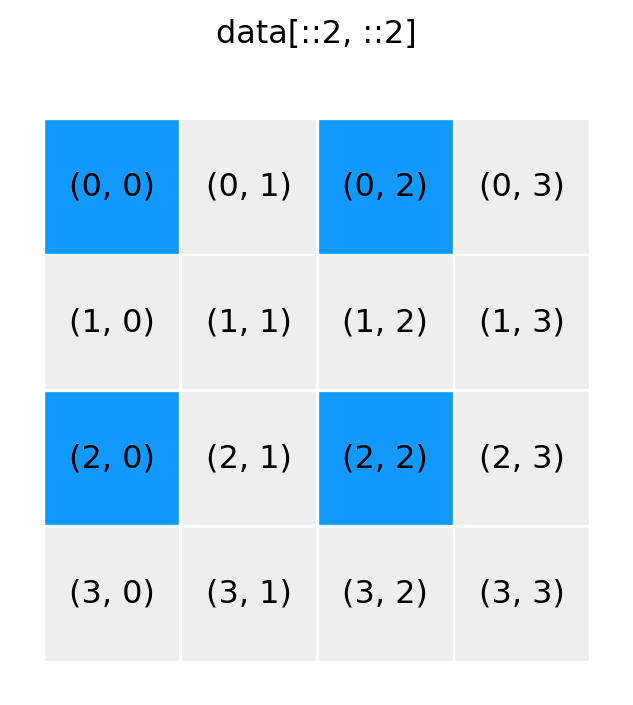

show_array((4, 4), '1::2, 1::2')

show_array((4, 4), ':, [0, 3]')

show_array((4, 4), '[1, 3], [0, 3]')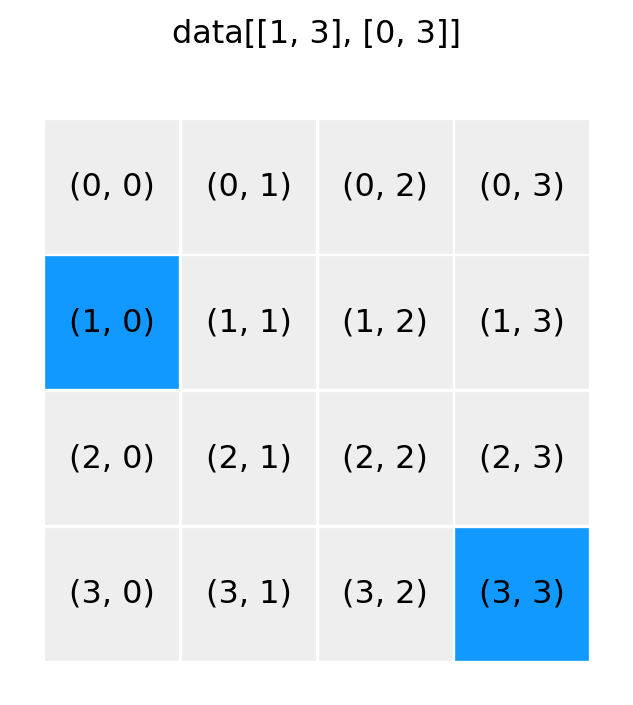

show_array((4, 4), ':, [False, True, True, False]')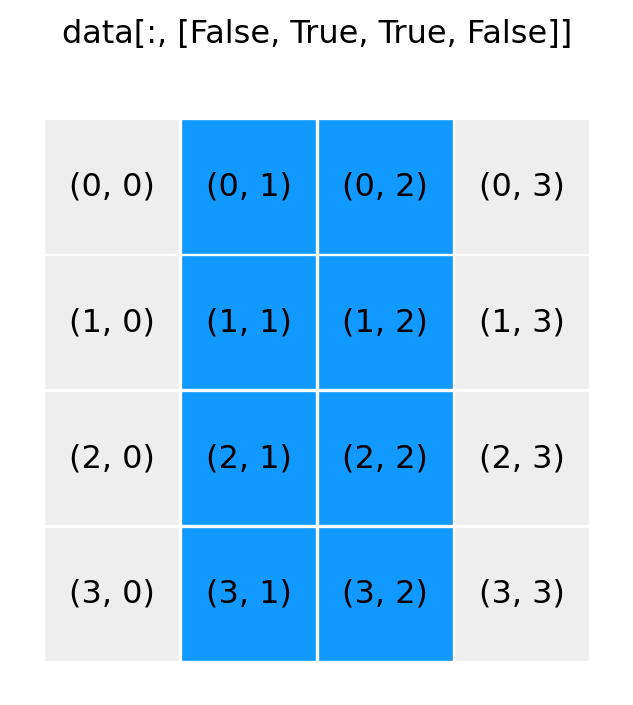

show_array((4, 4), '1:3, [False, True, True, False]')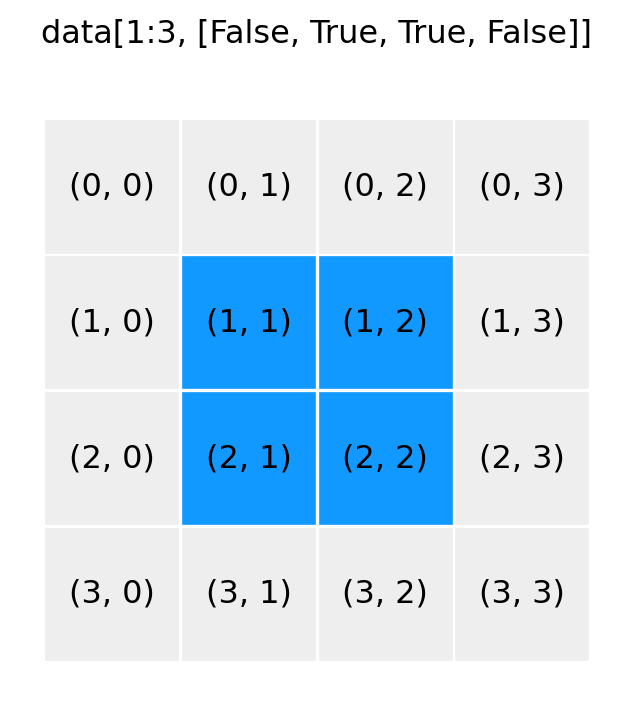

A.6 Reshaping and resizing

  • Reshaping an array does not require modifying the underlying array data; it only changes in how the data is interpreted, by redefining the array’s strides attribute
data = np.array([[1, 2], [3, 4]])
data1 = np.reshape(data, (1, 4))
data1
array([[1, 2, 3, 4]])
data1[0, 1] = -1
data
array([[ 1, -1],
       [ 3,  4]])
data2 = data.reshape(4)
data2
array([ 1, -1,  3,  4])
data2[1] = -2
data
array([[ 1, -2],
       [ 3,  4]])
data = np.array([[1, 2], [3, 4]])
data1 = np.ravel(data)
data1
array([1, 2, 3, 4])
data1[0] = -1
data
array([[-1,  2],
       [ 3,  4]])
  • The ndarray method flatten perform the same function, \(~\)but returns a copy instead of a view
data2 = data.flatten()
data2
array([-1,  2,  3,  4])
data2[0] = -2
data
array([[-1,  2],
       [ 3,  4]])
data = np.arange(0, 5)
data.shape
(5,)
column = data[:, np.newaxis]
column
array([[0],
       [1],
       [2],
       [3],
       [4]])
column.shape
(5, 1)
row = data[np.newaxis, :]
row
array([[0, 1, 2, 3, 4]])
row.shape
(1, 5)
row[0, 0] = -1
data
array([-1,  1,  2,  3,  4])
np.expand_dims(data, axis=1) 
array([[-1],
       [ 1],
       [ 2],
       [ 3],
       [ 4]])
row = np.expand_dims(data, axis=0)
row
array([[-1,  1,  2,  3,  4]])
row[0, 0] = 0
data
array([0, 1, 2, 3, 4])
data = np.arange(5)
data
array([0, 1, 2, 3, 4])
np.vstack((data, data, data))
array([[0, 1, 2, 3, 4],
       [0, 1, 2, 3, 4],
       [0, 1, 2, 3, 4]])
np.hstack((data, data, data))
array([0, 1, 2, 3, 4, 0, 1, 2, 3, 4, 0, 1, 2, 3, 4])
data = data[:, np.newaxis]
data.shape
(5, 1)
np.hstack((data, data, data))
array([[0, 0, 0],
       [1, 1, 1],
       [2, 2, 2],
       [3, 3, 3],
       [4, 4, 4]])
data1 = np.array([[1, 2], [3, 4]])
data2 = np.array([[5, 6]])
np.concatenate((data1, data2), axis=0)
array([[1, 2],
       [3, 4],
       [5, 6]])
np.concatenate((data1, data2.T), axis=1)
array([[1, 2, 5],
       [3, 4, 6]])

A.7 Vectorized expressions

A.7.1 Arithmetic operations

x = np.array([[1, 2], [3, 4]])
y = np.array([[5, 6], [7, 8]])
x + y
array([[ 6,  8],
       [10, 12]])
y - x
array([[4, 4],
       [4, 4]])
x * y
array([[ 5, 12],
       [21, 32]])
y / x
array([[5.        , 3.        ],
       [2.33333333, 2.        ]])
x * 2
array([[2, 4],
       [6, 8]])
2**x
array([[ 2,  4],
       [ 8, 16]])
y / 2
array([[2.5, 3. ],
       [3.5, 4. ]])
(y / 2).dtype
dtype('float64')

A.7.2 Broadcasting

a = np.array([[11, 12, 13], [21, 22, 23], [31, 32, 33]])
b = np.array([[1, 2, 3]])
a + b
array([[12, 14, 16],
       [22, 24, 26],
       [32, 34, 36]])
show_array_broadcasting(a, b)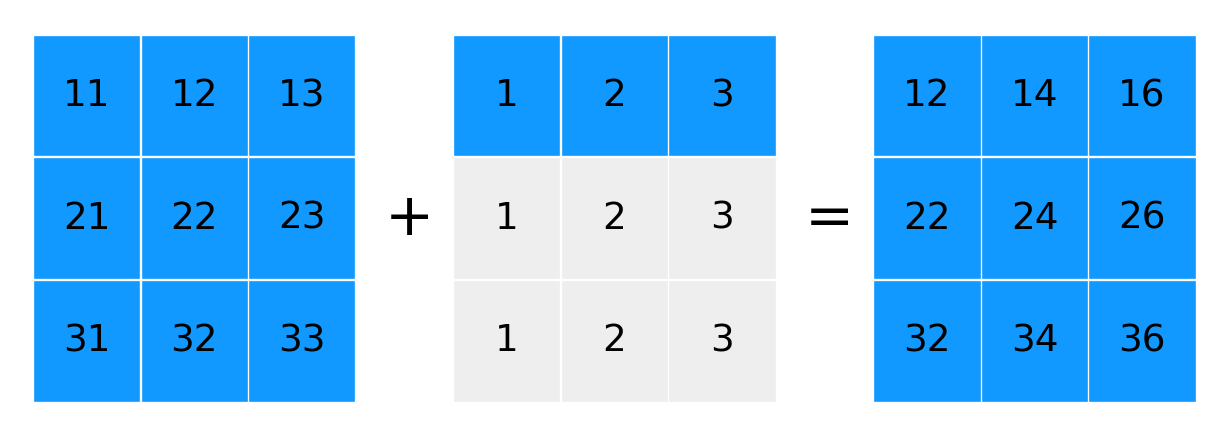

a + b.T
array([[12, 13, 14],
       [23, 24, 25],
       [34, 35, 36]])
show_array_broadcasting(a, b.T)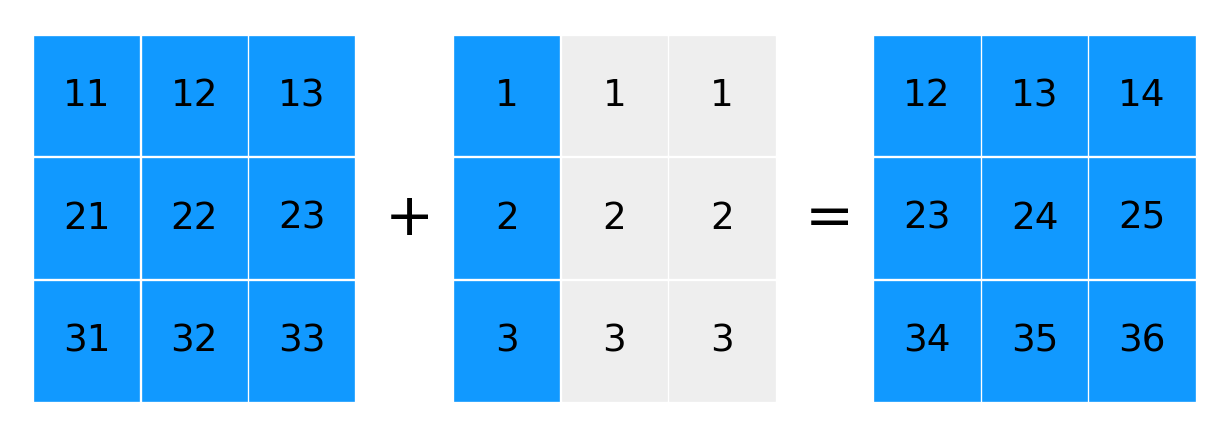

x = np.array([1, 2, 3, 4]).reshape(2, 2)
x.shape
(2, 2)
z = np.array([[2, 4]])
z.shape
(1, 2)
x / z
array([[0.5, 0.5],
       [1.5, 1. ]])
zz = np.vstack((z, z))
zz
array([[2, 4],
       [2, 4]])
x / zz
array([[0.5, 0.5],
       [1.5, 1. ]])
z = np.array([[2], [4]])
z.shape
(2, 1)
x / z
array([[0.5 , 1.  ],
       [0.75, 1.  ]])
zz = np.concatenate([z, z], axis=1)
zz
array([[2, 2],
       [4, 4]])
x / zz
array([[0.5 , 1.  ],
       [0.75, 1.  ]])
x = z = np.array([1, 2, 3, 4])
y = np.array([5, 6, 7, 8])
x = x + y  # x is reassigned to a new array
x, z
(array([ 6,  8, 10, 12]), array([1, 2, 3, 4]))
x = z = np.array([1, 2, 3, 4])
y = np.array([5, 6, 7, 8])
x += y  # the values of array x are updated in place
x, z
(array([ 6,  8, 10, 12]), array([ 6,  8, 10, 12]))

A.7.3 Elementwise functions

x = np.linspace(-1, 1, 11)
x
array([-1. , -0.8, -0.6, -0.4, -0.2,  0. ,  0.2,  0.4,  0.6,  0.8,  1. ])
y = np.sin(np.pi * x)
np.round(y, decimals=4)
array([-0.    , -0.5878, -0.9511, -0.9511, -0.5878,  0.    ,  0.5878,
        0.9511,  0.9511,  0.5878,  0.    ])
np.add(np.sin(x)**2, np.cos(x)**2)
array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
np.sin(x)**2 + np.cos(x)**2
array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.])
def heaviside(x):
    return 1 if x > 0 else 0
heaviside(-1)
0
heaviside(1.5)
1
```{python}
x = np.linspace(-5, 5, 11)
heaviside(x)
```

ValueError 
      1 x = np.linspace(-5, 5, 11)
----> 2 heaviside(x)

      1 def heaviside(x):
----> 2     return 1 if x > 0 else 0

ValueError: The truth value of an array with more than 
one element is ambiguous. Use a.any() or a.all()
heaviside = np.vectorize(heaviside)
heaviside(x)
array([0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1])
def heaviside(x):  # much better way
    return 1 * (x > 0)

heaviside(x)
array([0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1])

A.7.4 Aggregation

data = np.random.normal(size=(15, 15)) 
np.mean(data)
np.float64(-0.041673140354896374)
data.mean()
np.float64(-0.041673140354896374)
data = np.random.normal(size=(5, 10, 15))
data.sum(axis=0).shape
(10, 15)
data.sum(axis=(0, 2)).shape
(10,)
data.sum()
np.float64(18.68747786875952)
data = np.arange(9).reshape(3, 3)
data
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])
data.sum()
np.int64(36)
show_array_aggregation(data, None)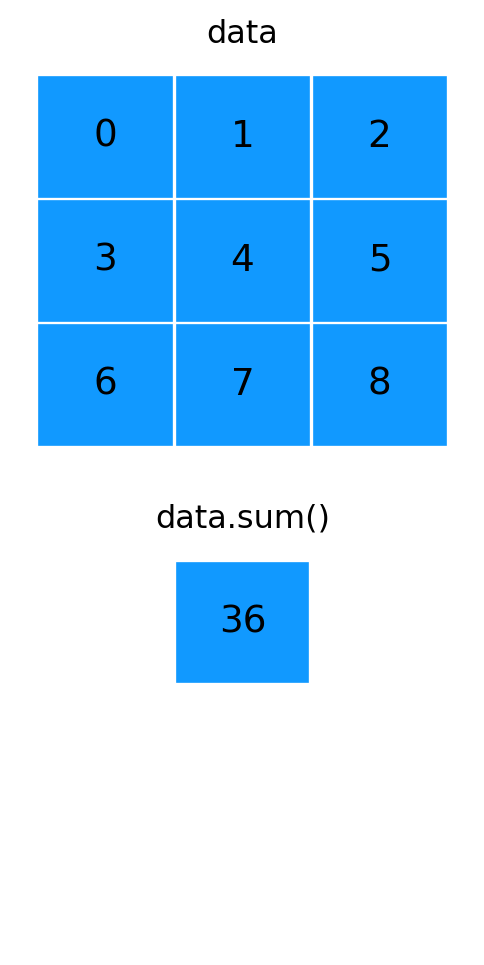

data.sum(axis=0)
array([ 9, 12, 15])
show_array_aggregation(data, 0)

data.sum(axis=1)
array([ 3, 12, 21])
show_array_aggregation(data, 1)

A.7.5 Boolean arrays and conditional expressions

a = np.array([1, 2, 3, 4])
b = np.array([4, 3, 2, 1])
a < b
array([ True,  True, False, False])
np.all(a < b)
np.False_
np.any(a < b)
np.True_
x = np.array([-2, -1, 0, 1, 2])
x > 0
array([False, False, False,  True,  True])
1 * (x > 0)
array([0, 0, 0, 1, 1])
x * (x > 0)
array([0, 0, 0, 1, 2])
def pulse(x, position, height, width):
    return height * (x >= position) * (x <= (position + width))  
x = np.linspace(-5, 5, 31)
pulse(x, position=-2, height=1, width=5)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,
       1, 1, 1, 0, 0, 0, 0, 0, 0])
pulse(x, position=1, height=2, width=2)
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 2, 2, 2, 2,
       2, 2, 2, 0, 0, 0, 0, 0, 0])
x = np.linspace(-4, 4, 9)
x
array([-4., -3., -2., -1.,  0.,  1.,  2.,  3.,  4.])
np.where(x < 0, x**2, x**3)
array([16.,  9.,  4.,  1.,  0.,  1.,  8., 27., 64.])
np.select([x < -1, x < 2, x>= 2], [x**2, x**3, x**4])
array([ 16.,   9.,   4.,  -1.,   0.,   1.,  16.,  81., 256.])
np.choose([0, 0, 0, 1, 1, 1, 2, 2, 2], [x**2, x**3, x**4])
array([ 16.,   9.,   4.,  -1.,   0.,   1.,  16.,  81., 256.])
x[np.abs(x) > 2]
array([-4., -3.,  3.,  4.])

A.7.6 Set operations

a = np.unique([1, 2, 3, 3])
a
array([1, 2, 3])
b = np.unique([2, 3, 4, 4, 5, 6, 5])
b
array([2, 3, 4, 5, 6])
np.in1d(a, b)
/var/folders/4x/8kn2nym12cn7x7qmg_6s4b8h0000gn/T/ipykernel_76845/924698060.py:1: DeprecationWarning: `in1d` is deprecated. Use `np.isin` instead.
  np.in1d(a, b)
array([False,  True,  True])
1 in a, 1 in b
(True, False)
np.all(np.in1d(a, b))  # to test if a is a subset of b
/var/folders/4x/8kn2nym12cn7x7qmg_6s4b8h0000gn/T/ipykernel_76845/423008062.py:1: DeprecationWarning: `in1d` is deprecated. Use `np.isin` instead.
  np.all(np.in1d(a, b))  # to test if a is a subset of b
np.False_
np.union1d(a, b)
array([1, 2, 3, 4, 5, 6])
np.intersect1d(a, b)
array([2, 3])
np.setdiff1d(a, b)
array([1])
np.setdiff1d(b, a)
array([4, 5, 6])

A.7.7 Operations on arrays

data = np.arange(9).reshape(3, 3)
data
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])
np.transpose(data)
array([[0, 3, 6],
       [1, 4, 7],
       [2, 5, 8]])
data = np.random.randn(1, 2, 3, 4, 5)
data.shape
(1, 2, 3, 4, 5)
data.T.shape
(5, 4, 3, 2, 1)

A.8 Matrix and vector operations

A = np.arange(1, 7).reshape(2, 3)
A
array([[1, 2, 3],
       [4, 5, 6]])
B = np.arange(1, 7).reshape(3, 2)
B
array([[1, 2],
       [3, 4],
       [5, 6]])
np.dot(A, B)
array([[22, 28],
       [49, 64]])
np.dot(B, A)
array([[ 9, 12, 15],
       [19, 26, 33],
       [29, 40, 51]])
A @ B  # python 3.5 above
array([[22, 28],
       [49, 64]])
B @ A
array([[ 9, 12, 15],
       [19, 26, 33],
       [29, 40, 51]])
A = np.arange(9).reshape(3, 3)
A
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])
x = np.arange(3)
x
array([0, 1, 2])
np.dot(A, x)
array([ 5, 14, 23])
A.dot(x)
array([ 5, 14, 23])
A @ x
array([ 5, 14, 23])
A = np.random.rand(3, 3)
B = np.random.rand(3, 3)
Ap = np.dot(B, np.dot(A, np.linalg.inv(B)))
Ap = B.dot(A.dot(np.linalg.inv(B)))
B @ A @ np.linalg.inv(B)
array([[-2.37625054,  0.83934428,  4.20566574],
       [-0.53237348,  0.16362199,  4.63972309],
       [-2.04694973,  0.71992986,  2.77055746]])
np.inner(x, x)
np.int64(5)
np.dot(x, x)
np.int64(5)
y = x[:, np.newaxis]
y
array([[0],
       [1],
       [2]])
np.dot(y.T, y)
array([[5]])
  • Given two vectors, \(\mathbf{a} = [a_0, a_1, ..., a_M]~\) and \(~\mathbf{b} = [b_0, b_1, ..., b_N]\), \(~\)the outer product is \(\mathbf{a}^T\mathbf{b}\)

\[\begin{pmatrix} a_0 b_0 & a_0b_1 & \cdots & a_0 b_N \\ a_1 b_0 & \cdots & \cdots & a_1 b_N \\ \vdots & \ddots & & \vdots \\ a_M b_0 & & \ddots & a_M b_N \\ \end{pmatrix} \]

x = np.array([1, 2, 3])
np.outer(x, x)
array([[1, 2, 3],
       [2, 4, 6],
       [3, 6, 9]])
np.kron(x, x)
array([1, 2, 3, 2, 4, 6, 3, 6, 9])
np.kron(x[:, np.newaxis], x[np.newaxis, :])
array([[1, 2, 3],
       [2, 4, 6],
       [3, 6, 9]])
np.kron(np.ones((2, 2)), np.identity(2))
array([[1., 0., 1., 0.],
       [0., 1., 0., 1.],
       [1., 0., 1., 0.],
       [0., 1., 0., 1.]])
np.kron(np.identity(2), np.ones((2, 2)))
array([[1., 1., 0., 0.],
       [1., 1., 0., 0.],
       [0., 0., 1., 1.],
       [0., 0., 1., 1.]])
x = np.array([1, 2, 3, 4])
y = np.array([5, 6, 7, 8])
np.einsum("n,n", x, y)
np.int64(70)
np.inner(x, y)
np.int64(70)
A = np.arange(9).reshape(3, 3)
B = A.T
np.einsum("mk,kn", A, B)
array([[  5,  14,  23],
       [ 14,  50,  86],
       [ 23,  86, 149]])
np.all(np.einsum("mk,kn", A, B) == np.dot(A, B))
np.True_