8  Vectors

8.1 Vectors in 2-Space

• We distinguish two important quantities: \(~\) scalars and vectors

  • A scalar is simply a real number or a quantity that has magnitude
  • A vector is usually described as a quantity that has both magnitude and direction

• Equal, Scalar Multiplication

  \(~\)

  

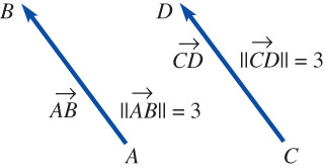
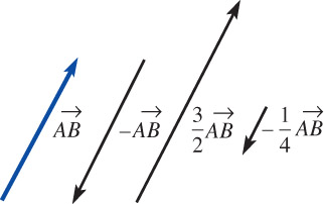
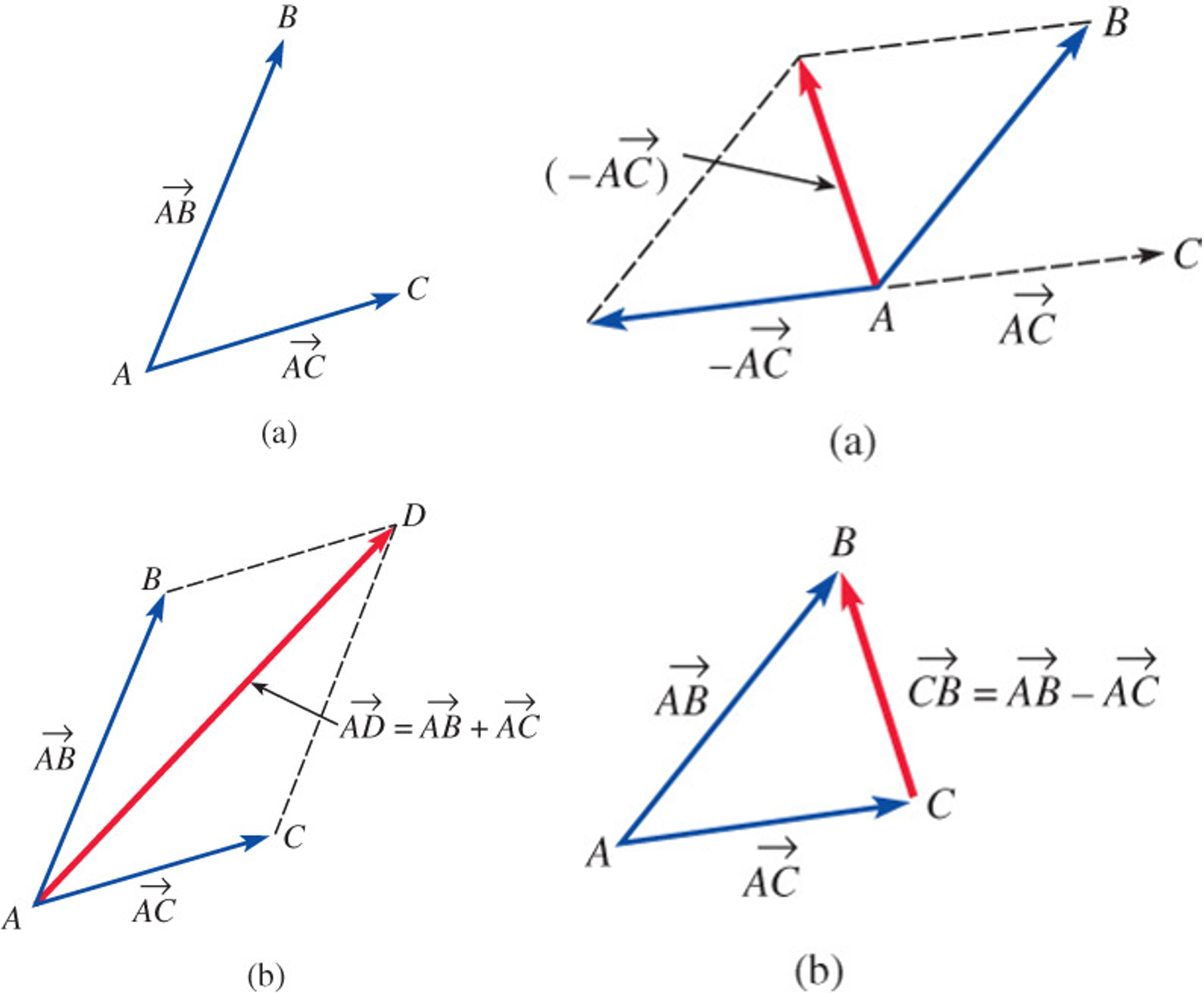
• Addition and Subtraction

  \(~\)

• Vectors in a Coordinate Plane

  \[\mathbf{a}=\left \langle a_1, a_2 \right \rangle\]

  

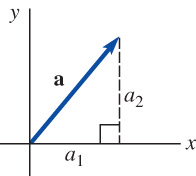
• Let \(~\)\(\mathbf{a}=\left \langle a_1, a_2 \right \rangle~\) and \(~\)\(\mathbf{b}=\left \langle b_1, b_2 \right \rangle~\) be vectors in \(\mathbb{R}^2\)

  • Equality: \(\text{ }\) \(\mathbf{a} =\mathbf{b}~\) if and only if \(~a_1 =b_1, \;a_2=b_2\)
  • Addition: \(\text{ }\) \(\mathbf{a} +\mathbf{b} =\left \langle a_1 +b_1, a_2 +b_2 \right \rangle\)
  • Scalar multiplication: \(\text{ }\) \(k\mathbf{a} =\left \langle k a_1, k a_2 \right \rangle\)

• Properties of Vectors

  • \(\mathbf{a} +\mathbf{b} = \mathbf{b} +\mathbf{a}\)

  • \(\mathbf{a} +(\mathbf{b} +\mathbf{c}) = (\mathbf{a} +\mathbf{b}) +\mathbf{c}\)

  • \(\mathbf{a} +\mathbf{0} = \mathbf{a}\)

  • \(\mathbf{a} +(-\mathbf{a}) = \mathbf{0}\)

  • \(k(\mathbf{a} +\mathbf{b}) = k\mathbf{a} +k\mathbf{b}\)

  • \((k_1 +k_2)\mathbf{a} = k_1\mathbf{a} +k_2\mathbf{a}\)

  • \(k_1(k_2 \mathbf{a}) = (k_1 k_2) \mathbf{a}\)

  • \(1\mathbf{a} = \mathbf{a}\)

  • \(0\mathbf{a} = \mathbf{0}\)

• Magnitude, \(\,\) Unit Vector

  \(\begin{aligned} \left \| \mathbf{a} \right \| &= \sqrt{a_1^2 +a_2^2} \;\;\text{ for }\; \mathbf{a} =\left \langle a_1, a_2 \right \rangle \\ \mathbf{u} &= \frac{\mathbf{a}}{\left \| \mathbf{a} \right \|} \end{aligned}\)

• \(\mathbf{i}\), \(~\mathbf{j}\) vectors

  \(\begin{aligned} \mathbf{a} &= \left \langle a_1, a_2 \right \rangle \\ &=\left \langle a_1, 0 \right \rangle +\left \langle 0, a_2 \right \rangle \\ &= a_1 \left \langle 1, 0 \right \rangle +a_2 \left \langle 0, 1 \right \rangle \\ &= a_1 \mathbf{i} +a_2 \mathbf{j} \end{aligned}\)

\(~\)

Example \(\,\) Use the given figure to prove the given result

\[\mathbf{a} +\mathbf{b} +\mathbf{c}=\mathbf{0}\;~\text{and}\;~\mathbf{a} +\mathbf{b} +\mathbf{c} +\mathbf{d}=\mathbf{0}\]

\(~\)

8.2 Vectors in 3-Space

\(~\)

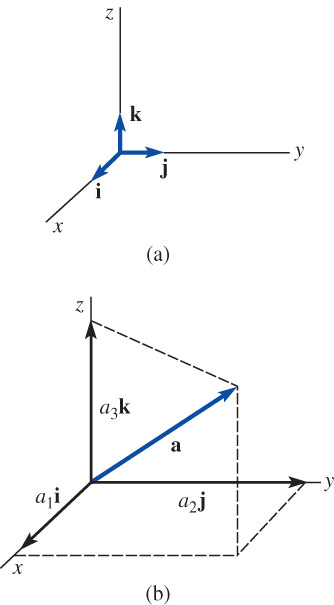
• \(\mathbf{i}\), \(~\mathbf{j}\), and \(~\mathbf{k}\) vectors

  \(\begin{aligned} \mathbf{a} &= \left \langle a_1, a_2, a_3 \right \rangle \\ &= \left \langle a_1, 0, 0 \right \rangle +\left \langle 0, a_2, 0 \right \rangle +\left \langle 0, 0, a_3 \right \rangle \\ &= a_1 \left \langle 1, 0, 0 \right \rangle +a_2 \left \langle 0, 1, 0 \right \rangle +a_3 \left \langle 0, 0, 1 \right \rangle \\ &= a_1 \mathbf{i} +a_2 \mathbf{j} +a_3 \mathbf{k} \end{aligned}\)

• Octants

\(~\)

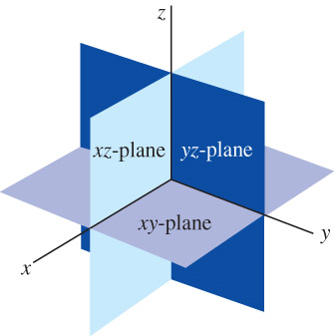
Axes	Coordinates	Plane	Coordinates
\(x\)	\((a, 0, 0)\)	\(xy\)	\((a, b, 0)\)
\(y\)	\((0, b, 0)\)	\(yz\)	\((0, b, c)\)
\(z\)	\((0, 0, c)\)	\(xz\)	\((a, 0, c)\)

\(~\)

\(~\)

• Let \(\,\mathbf{a}=\left \langle a_1, a_2, a_3 \right \rangle\,\) and \(\,\mathbf{b}=\left \langle b_1, b_2, b_3 \right \rangle\) be vectors in \(\mathbb{R}^3\)

  • Equality: \(~\mathbf{a} =\mathbf{b}~\text{ if and only if }~a_1 =b_1, \;a_2=b_2, \;a_3=b_3\)
  • Addition: \(~\mathbf{a} +\mathbf{b} =\left \langle a_1 +b_1, a_2 +b_2, a_3 +b_3 \right \rangle\)
  • Scalar multiplication: \(~k\mathbf{a} =\left \langle k a_1, k a_2, k a_3 \right \rangle\)
  • Negative: \(-\mathbf{b} =(-1)\mathbf{b} =\left \langle -b_1, -b_2, -b_3 \right \rangle\)
  • Subtraction: \(~\mathbf{a} -\mathbf{b} = \mathbf{a} +(-1)\mathbf{b} =\left \langle a_1 -b_1, a_2 -b_2, a_3 -b_3 \right \rangle\)
  • Zero vector: \(~\mathbf{0} =\left \langle 0, 0, 0 \right \rangle\)
  • Magnitude: \(~\left \| \mathbf{a} \right \| =\sqrt{a_1^2 +a_2^2 +a_3^2}\)

\(~\)

Example \(\,\) Describe the locus of points \(P(x, y, z)\) that satisfy the given equations

• \(xyz=0\)

• \((x+1)^2 +(y-2)^2 +(z+3)^2 = 0\)

• \((x-2)(z-8)=0\)

• \(z^2 -25=0\)

• \(x=y=z\)

\(~\)

8.3 Dot Product (Inner or Scalar Product)

• The dot product of \(\mathbf{a}=\left \langle a_1, a_2, a_3 \right \rangle\) and \(\mathbf{b}=\left \langle b_1, b_2, b_3 \right \rangle\) is

  \(\phantom{x}\mathbf{a} \cdot \mathbf{b} = a_1 b_1 + a_2 b_2 + a_3 b_3\)

• Properties of the Dot Product

  • \(\mathbf{a}\cdot\mathbf{b} = 0~\) if \(~\mathbf{a}=\mathbf{0}~\) or \(~\mathbf{b}=\mathbf{0}\)
  • \(\mathbf{a}\cdot\mathbf{b} = \mathbf{b}\cdot\mathbf{a}\)
  • \(\mathbf{a}\cdot(\mathbf{b} +\mathbf{c}) = \mathbf{a}\cdot\mathbf{b} +\mathbf{a}\cdot\mathbf{c}\)
  • \(\mathbf{a}\cdot(k\mathbf{b}) = (k\mathbf{a})\cdot\mathbf{b} =k(\mathbf{a}\cdot\mathbf{b})\)
  • \(\mathbf{a}\cdot\mathbf{a} \geq 0\)
  • \(\mathbf{a}\cdot\mathbf{a} =\left \| \mathbf{a} \right \|^2\)

• Alternative Form

  The dot product of two vectors \(\mathbf{a}\) and \(\mathbf{b}\) is

  \(\phantom{xx}\mathbf{a}\cdot\mathbf{b} =\left\| \mathbf{a} \right\| \left\| \mathbf{b} \right\| \cos\theta\)

  where \(\theta\) is the angle between the vectors, \(\,0 \leq \theta \leq \pi\)

• Angle between two vectors

  \(\displaystyle\phantom{xx}\cos\theta = \frac{a_1 b_1 +a_2 b_2 + a_3 b_3}{\left\| \mathbf{a}\right\| \left\| \mathbf{b}\right\|}\)

  • Direction cosines

  

  \(\phantom{xx}\displaystyle\cos\alpha=\frac{a_1}{\left\|\mathbf{a}\right\|}\), \(~\displaystyle\cos\beta=\frac{a_2}{\left\|\mathbf{a}\right\|}\), \(~\displaystyle\cos\gamma=\frac{a_3}{\left\|\mathbf{a}\right\|}\)

• Orthogonal vectors

  Two nonzero vectors \(\mathbf{a}\) and \(\mathbf{b}\) are orthogonal if and only if \(~\mathbf{a}\cdot\mathbf{b}=0\)

• Component of \(\mathbf{a}\) on \(\mathbf{b}\)

  To find the component of \(\mathbf{a}\) on a vector \(\mathbf{b}\), \(~\)we dot \(\mathbf{a}\) with a unit vector in the direction of \(\mathbf{b}\)

  

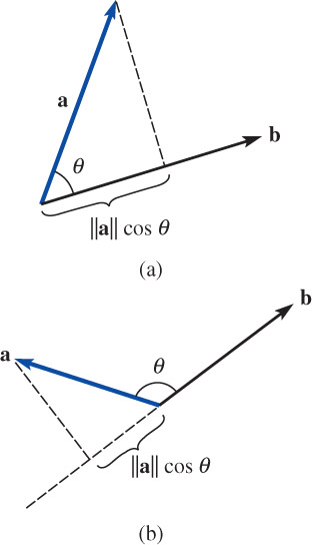
  \[\text{comp}_{\mathbf{b}} \mathbf{a} =\left\| \mathbf{a} \right\| \cos\theta =\left\| \mathbf{a} \right\| \cos\theta \frac{\left\| \mathbf{b} \right\|}{\left\| \mathbf{b} \right\|} =\frac{\mathbf{a}\cdot\mathbf{b}}{\left\| \mathbf{b} \right\|} =\mathbf{a} \cdot\frac{\mathbf{b}}{\left\| \mathbf{b} \right\|}\]

• Projection of \(\mathbf{a}\) onto \(\mathbf{b}\)

  

  \[\text{proj}_{\mathbf{b}} \mathbf{a} = \left(\text{comp}_{\mathbf{b}} \mathbf{a} \right) \left(\frac{\mathbf{b}}{\left\| \mathbf{b} \right\|} \right)=\color{red}{\left(\frac{\mathbf{a}\cdot\mathbf{b}}{\mathbf{b}\cdot\mathbf{b}}\right) \mathbf{b}}\]

\(~\)

Example \(\,\) Verify that the vector \(\displaystyle \mathbf{c}=\mathbf{b} - \left(\frac{\mathbf{a} \cdot \mathbf{b}}{\mathbf{a} \cdot \mathbf{a}}\right) \mathbf{a}\,\) is orthogonal to the vector \(\mathbf{a}\)

\(~\)

Example \(\,\) In the methane molecule \(\mathrm{CH}_4\), the hydrogen atoms are located at the four vertices of a regular tetrahedron. The distance between the center of a hydrogen atom and the center of a carbon atom is 1.10 angstroms, and the hydrogen-carbon-hydrogen bond angle is \(\,\theta=109.5^\circ\). Using vector methods only, find the distance between two hydrogen atoms

\(~\)

8.4 Cross Product

• Cross product of Two vectors

  \(\phantom{xx}\mathbf{a} \times \mathbf{b} =\left|\begin{matrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \end{matrix}\right| =\left|\begin{matrix} a_2 & a_3\\ b_2 & b_3 \end{matrix}\right| \mathbf{i} -\left|\begin{matrix} a_1 & a_3\\ b_1 & b_3 \end{matrix}\right| \mathbf{j} +\left|\begin{matrix} a_1 & a_2\\ b_1 & b_2 \end{matrix}\right| \mathbf{k}\)

• Alternative Form and Magnitude of the Cross Product

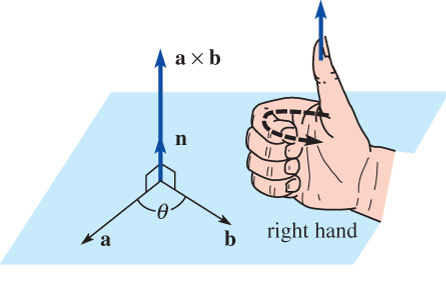
  \(\phantom{xx}\mathbf{a}\times\mathbf{b} =(\left\| \mathbf{a} \right\| \left\| \mathbf{b} \right\| \sin\theta)\,\mathbf{n} =\left\| \mathbf{a}\times\mathbf{b} \right\| \mathbf{n}\)

• Right-Hand Rule

  The vectors \(\mathbf{a}\), \(\mathbf{b}\), and \(~\mathbf{a}\times\mathbf{b}~\) form a right-hand system:

  

• Parallel Vectors

  Two nonzero vectors \(\mathbf{a}\) and \(\mathbf{b}\) are parallel if and only if \(~\mathbf{a}\times\mathbf{b}=\mathbf{0}\)

• Properties of the Cross Product \(~\)

  • \(\mathbf{a}\times\mathbf{b} = \mathbf{0}~\) if \(~\mathbf{a}=\mathbf{0}~\) or \(~\mathbf{b}=\mathbf{0}\)
  • \(\mathbf{a}\times\mathbf{b} =-\mathbf{b}\times\mathbf{a}\)
  • \(\mathbf{a}\times(\mathbf{b} +\mathbf{c}) = (\mathbf{a}\times\mathbf{b}) +(\mathbf{a}\times\mathbf{c})\)
  • \((\mathbf{a} +\mathbf{b}) \times\mathbf{c} = (\mathbf{a}\times\mathbf{c}) +(\mathbf{b}\times\mathbf{c})\)
    
  • \(\mathbf{a}\times(k\mathbf{b}) = (k\mathbf{a})\times\mathbf{b} =k(\mathbf{a}\times\mathbf{b})\)
  • \(\mathbf{a}\times\mathbf{a} =\mathbf{0}\)
  • \(\mathbf{a}\cdot(\mathbf{a}\times\mathbf{b})=0\)
  • \(\mathbf{b}\cdot(\mathbf{a}\times\mathbf{b})=0\)

• Areas of a parallelogram and a Trianlge

  \(\text{(a)}\) \(~A =\left\|\mathbf{a} \times \mathbf{b} \right\|\)

  \(\text{(b)}\) \(~A =\frac{1}{2}\left\|\mathbf{a} \times \mathbf{b} \right\|\)

  \(~\)

  

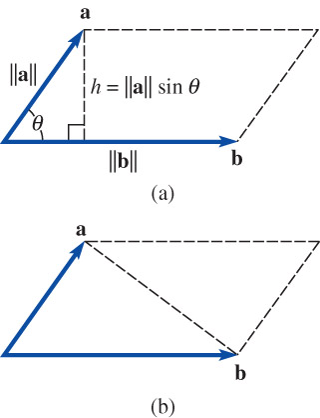
• Volume of a Parallelepiped

  \(\phantom{xx}V=\left| \mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})\right|\)

  \(~\)

  

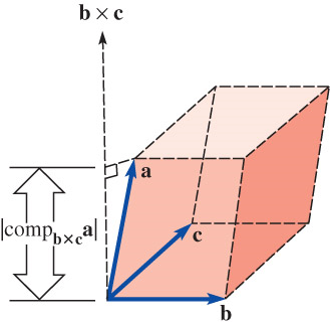
• Special Products

  \(\phantom{xx}\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}) = \left|\begin{matrix} a_1 & a_2 & a_3\\ b_1 & b_2 & b_3\\ c_1 & c_2 & c_3 \end{matrix}\right| = (\mathbf{a} \times \mathbf{b}) \cdot \mathbf{c}\)

  \(~\)

  \(\phantom{xx}\mathbf{a} \times (\mathbf{b} \times \mathbf{c}) = (\mathbf{a} \cdot \mathbf{c}) \mathbf{b} -(\mathbf{a} \cdot \mathbf{b}) \mathbf{c}\)

\(~\)

Example \(\,\) Prove or disprove

• \(~\mathbf{a} \times (\mathbf{b} \times \mathbf{c}) = (\mathbf{a} \cdot \mathbf{c}) \mathbf{b} -(\mathbf{a} \cdot \mathbf{b}) \mathbf{c}\)

• \(~\mathbf{a} \times (\mathbf{b} \times \mathbf{c}) =(\mathbf{a} \times \mathbf{b}) \times \mathbf{c}\)

• \(~\mathbf{a} \times (\mathbf{b} \times \mathbf{c}) +\mathbf{b} \times (\mathbf{c} \times \mathbf{a}) +\mathbf{c} \times (\mathbf{a} \times \mathbf{b})=\mathbf{0}\)

• Lagrange’s identity \(\| \mathbf{a}\times\mathbf{b}\|^2 = \|\mathbf{a}\|^2 \|\mathbf{b}\|^2 - (\mathbf{a}\cdot\mathbf{b})^2\)

\(~\)

8.5 Lines and Planes in 3-Space

• Lines

  

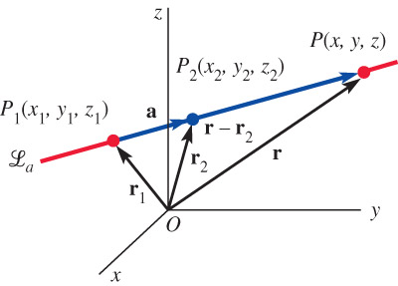
  \[ \begin{aligned} \mathbf{r} -\mathbf{r}_2 &= t(\mathbf{r}_2 - \mathbf{r}_1) = t\mathbf{a}=t \left \langle x_2 -x_1, y_2 -y_1, z_2 -z_1 \right \rangle \\ &\Rightarrow \;\displaystyle t = \frac{x - x_2}{a_1} = \frac{y - y_2}{a_2} = \frac{z - z_2}{a_3} \end{aligned}\]

• Planes

  If the normal vector is \(\mathbf{n}=a\mathbf{i} +b\mathbf{j} +c\mathbf{k}\), \(~\)then

  \[\mathbf{n}\cdot(\mathbf{r} -\mathbf{r}_1)=0 ~\Rightarrow~ a(x -x_1) +b (y -y_1) +c(z- z_1)=0\]

  

  

\(~\)

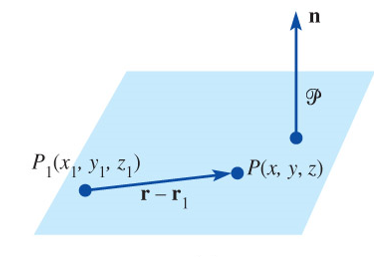
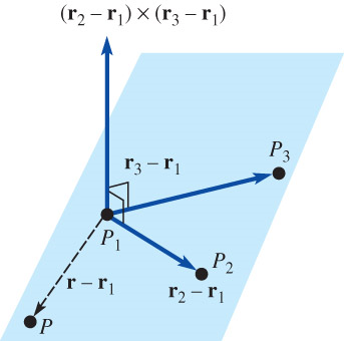
Example \(\,\) Find parametric equation for the line that contains \((-4, 1, 7)\) and is perpendicular to the plane \[-7x+2y+3z=1\]

\(~\)

Example \(\,\) Find parametric equations for the line of intersection of the given planes

\[ \begin{aligned} 5x - 4y -9z &= 8\\ x + 4y +3z &= 4 \end{aligned}\]

\(~\)

Example \(\,\) Find an equation of the plane that contains the given line and is orthogonal to the indicated plane

\[\frac{2-x}{3}=\frac{y+2}{5}=\frac{z-8}{2}; \quad 2x - 4y-z + 16=0\]

\(~\)

8.6 Vector Spaces

• \(n\)-Space

  • A vector in n-space is any ordered \(n\)-tuple \(\,\mathbf{a}=\left\langle a_1, a_2, \cdots, a_n \right\rangle\) of real numbers called the components of \(~\mathbf{a}\)
  • The set of all vectors in \(n\)-space is denoted by \(\mathbb{R}^n\)
  • The component definitions in 3-space carry over to \(\mathbb{R}^n\)
    in a natural way

• The standard dot or inner product of two \(n\)-vectors is the real number defined by

  \(\phantom{xx}\begin{aligned} \mathbf{a} \cdot \mathbf{b} &= \left\langle a_1, a_2, \cdots, a_n \right\rangle \cdot \left\langle b_1, b_2, \cdots, b_n \right\rangle \\ &= a_1 b_1 +a_2 b_2 + \cdots + a_n b_n \end{aligned}\)

• Two nonzero vectors \(\mathbf{a}\) and \(\mathbf{b}\) in \(\mathbb{R}^n\) are said to be orthogonal if and only if \(~\mathbf{a} \cdot \mathbf{b} = 0\)

• Vector Space

  Let \(V\) be a set of elements on which two operations called vector addition and scalar multiplication are defined. Then \(V\) is said to be a vector space if the following 10 properties are satisfied

• Axioms for Vector Addition

  • If \(\mathbf{x}\) and \(\mathbf{y}\) are in \(V\), \(~\)then \(\mathbf{x} +\mathbf{y}\) is in \(V\)

  • For all \(\mathbf{x}\), \(\mathbf{y}\) in \(V\), \(~\)\(\mathbf{x} +\mathbf{y} = \mathbf{y} +\mathbf{x}\)

  • For all \(\mathbf{x}\), \(\mathbf{y}\), \(\mathbf{z}\) in \(V\), \(~\)\(\mathbf{x} +(\mathbf{y} +\mathbf{z}) = (\mathbf{x} +\mathbf{y}) +\mathbf{z}\)

  • There is a unique vector \(\mathbf{0}\) in \(V\) such that \(~\)\(\mathbf{0} +\mathbf{x} = \mathbf{x} +\mathbf{0}\)

  • For each \(\mathbf{x}\) in \(V\), \(~\)there exists a vector \(=\mathbf{x}~\) such that \(\mathbf{x} +(-\mathbf{x}) = (-\mathbf{x}) +\mathbf{x} =\mathbf{0}\)

• Axioms for Scalar Multiplication

  • If \(k\) is any scalar and \(\mathbf{x}\) is in \(V\), \(~\)then \(~k\mathbf{x}~\) is in \(V\)

  • \(k(\mathbf{x} +\mathbf{y}) =k\mathbf{x} + k\mathbf{y}\)

  • \((k_1 +k_2)\mathbf{x} =k_1\mathbf{x} + k_2\mathbf{x}\)

  • \(k_1(k_2\mathbf{x})=(k_2k_2)\mathbf{x}\)

  • \(1\mathbf{x}=\mathbf{x}\)

• Here are some important vector spaces:

  • The set \(\mathbb{R}\) of real numbers

  • The set \(\mathbb{R}^2\) of ordered pairs

  • The set \(\mathbb{R}^3\) of ordered triples

  • The set \(\mathbb{R}^n\) of ordered \(n\)-tuples

  • The set \(P_n\) of polynomials of degree less than or equal to \(n\)

  • The set \(P\) of all polynomials

  • The set of real-valued functions \(~f\) defined on the set \(\mathbb{R}\)

  • The set \(C[a,b]\) of real-valued functions \(~f\) continuous on the closed interval \([a,b]\)

  • The set \(C(-\infty,\infty)\) of real-valued functions \(~f\) continuous on the set \(\mathbb{R}\)

  • The set \(C^n[a,b]\) of all real-valued functions \(~f\), \(\,\) for which \(f\), \(f'\), \(f''\), \(\cdots\), \(f^{(n)}\) exist and are continuous on the closed interval \([a,b]\)

\(~\)

Example \(\,\) Consider the set \(V\) of positive real numbers. If \(x\) and \(y\) denote positive real numbers, then we write vectors in \(V\) as \(\mathbf{x}=x~\) and \(~\mathbf{y}=y\)

• Now, \(~\) addition of vectors is defined by

  \(\phantom{xx}\mathbf{x} +\mathbf{y} =xy\)

• and scalar multiplication is defined by

  \(\phantom{xx}k\mathbf{x}=x^k\)

  Determine whether \(V\) is a vector space

\(~\)

• Subspace

  • A nonempty subset \(W\) of a vector space \(V\) is a subspace of \(V~\) if and only if \(~W\) is closed under vector addition and scalar multiplication defined on \(V\):

    • If \(\mathbf{x}\) and \(\mathbf{y}\) are in \(W\), \(~\)then \(\mathbf{x} +\mathbf{y}\) is in \(W\)
    • If \(\mathbf{x}\) is in \(W\) and \(k\) is any scalar, \(~\)then \(k\mathbf{x}\) is in \(W\)

• Linear Independence

  A set of vectors \(\left\{ \mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_n \right\}\) is said to be linearly indpenedent if the only constants satisfying the equation

  \[k_1\mathbf{x}_1 +k_2\mathbf{x}_2 +\cdots +k_n\mathbf{x}_n=\mathbf{0}\]

  are \(k_1=k_2=\cdots=k_n=0\). If the set of vectors is not linearly indpenedent, \(~\)then it is said to be linearly dependent

• Basis

  Consider a set of vectors \(B=\left\{\mathbf{x}_1, \mathbf{x}_2,\cdots,\mathbf{x}_n\right\}\,\) in a vector space \(V\). \(~\)If the set \(\,B\,\) is linearly independent and if every vector in \(V\) can be expressed as a linear combination of these vectors, \(~\)then \(B\) is said to be a basis in \(V\)

• Dimension

  The number of vectors in a basis \(\,B\,\) for a vector space \(~V\) is said to be the dimension of the space

• Span

  If \(S\) denotes any set of vectors \(\left\{\mathbf{x}_1, \mathbf{x}_2,\cdots,\mathbf{x}_n\right\}\) in a vector space \(V\), \(\,\)then the set of all linear combinations of the vector \(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n\) in \(S\),

  \[\left\{ k_1\mathbf{x}_1 +k_2\mathbf{x}_2+ \cdots+k_n\mathbf{x}_n\right\}\]

  where the \(k_i\) are scalars, \(\,\)is called the span of the vectors and written \(\mathrm{span}(S)\) or \(\mathrm{span}(\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_n)\)

  \(~\)

  If \(\,V=\text{span}(S)\), \(\,\)then we say that \(\,S\,\) is a spanning set for the vector space \(V\), \(\,\)or that \(\,S\,\) spans \(\,V\)

\(~\)

Example \(\,\) Determine whether the given set is a vector space:

• The set of complex numbers \(a + bi\), \(\,\)where \(i^2=-1\), \(\,\)addition and scalar multiplication defined by

  \[ \begin{aligned} (a_1 + b_1 i) +(a_2 +b_2 i) &= (a_1 +a_2) +(b_1 +b_2)i \\ k(a+bi) &= ka +kb i \end{aligned}\]

  where \(k\) is a real number

• The set of arrays of real numbers \(\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}\), \(~\) addition and scalar multiplication defined by

\[ \begin{aligned} \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} + \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix} &= \begin{pmatrix} a_{12} +b_{12} & a_{11}+b_{11} \\ a_{22} +b_{22} & a_{21}+b_{21} \end{pmatrix}\\ k\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix}&= \begin{pmatrix} ka_{11} & ka_{12} \\ ka_{21} & ka_{22} \end{pmatrix} \end{aligned}\]

\(~\)

8.7 Gram-Schmidt Orthogonalization Process

• Every vector \(\mathbf{u}\) in \(\mathbb{R}^n\) can be written as a linear combination of the vectors in the standard basis \(B=\left\{ \mathbf{e}_1, \mathbf{e}_2, \cdots, \mathbf{e}_n \right\}\):

  \[ \begin{aligned} \mathbf{e}_1 &=\left\langle 1,0,0,\cdots,0 \right\rangle \\ \mathbf{e}_2 &=\left\langle 0,1,0,\cdots,0 \right\rangle \\ &\;\;\vdots \\ \mathbf{e}_n &=\left\langle 0,0,0,\cdots,1 \right\rangle \end{aligned}\]

  This standard basis \(B=\left\{ \mathbf{e}_1, \mathbf{e}_2, \cdots, \mathbf{e}_n \right\}\,\) is also an example of an orthonormal basis

  \[\mathbf{e}_i \cdot \mathbf{e}_j = 0, \,i \neq j ~\text{ and}~ \left\| \mathbf{e}_i \right\|=1, ~i=1,2,\cdots,n\]

• Coordinates Relative to an Orthonormal Basis

  Suppose \(B=\left\{ \mathbf{w}_1, \mathbf{w}_2, \cdots, \mathbf{w}_n \right\}\) is an orthonormal basis for \(\mathbb{R}^n\). \(\,\)If \(\mathbf{u}\) is any vector in \(\mathbb{R}^n\), \(~\)then

  \[\mathbf{u} = (\mathbf{u}\cdot\mathbf{w}_1)\mathbf{w}_1 +(\mathbf{u}\cdot\mathbf{w}_2)\mathbf{w}_2 + \cdots +(\mathbf{u}\cdot\mathbf{w}_n)\mathbf{w}_n\]

• Constructing an Orthogonal Basis for \(\mathbb{R}^2\)

  \[\begin{aligned} \mathbf{v}_1 &= \mathbf{u}_1 \\ \mathbf{v}_2 &= \mathbf{u}_2 -\left( \frac{\mathbf{u}_2 \cdot \mathbf{v}_1}{\mathbf{v}_1 \cdot \mathbf{v}_1}\right) \mathbf{v}_1\end{aligned}\]

  

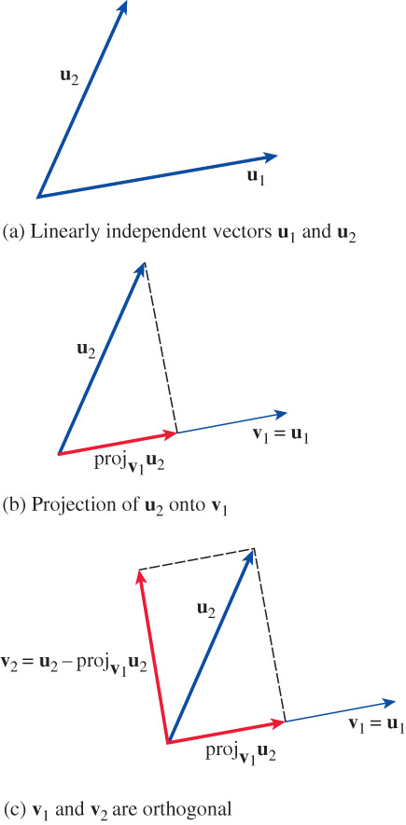
• Constructing an Orthogonal Basis for \(\mathbb{R}^3\)

  \[\begin{aligned} \mathbf{v}_1 &= \mathbf{u}_1 \\ \mathbf{v}_2 &= \mathbf{u}_2 -\left( \frac{\mathbf{u}_2 \cdot \mathbf{v}_1}{\mathbf{v}_1 \cdot \mathbf{v}_1}\right) \mathbf{v}_1 \\ \mathbf{v}_3 &= \mathbf{u}_3 -\left( \frac{\mathbf{u}_3 \cdot \mathbf{v}_1}{\mathbf{v}_1 \cdot \mathbf{v}_1}\right) \mathbf{v}_1 -\left( \frac{\mathbf{u}_3 \cdot \mathbf{v}_2}{\mathbf{v}_2 \cdot \mathbf{v}_2}\right) \mathbf{v}_2 \end{aligned}\]

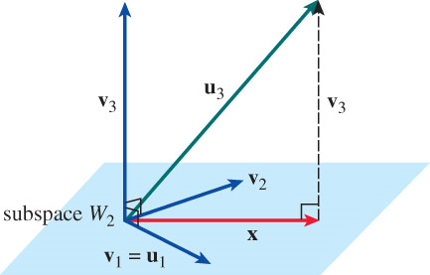
• Gram-Schmidt Orthogonalization Process

  Let \(\,B=\left\{ \mathbf{u}_1, \mathbf{u}_2, \cdots, \mathbf{u}_m \right\}\), \(~m \leq n\), \(~\)be a basis for a subspace \(W_m\) of \(~\mathbb{R}^n\). \(\,\)Then \(B'=\left\{ \mathbf{v}_1, \mathbf{v}_2, \cdots, \mathbf{v}_m \right\}\) , \(\,\)where

  \[ \begin{aligned} \mathbf{v}_1 & = \mathbf{u}_1 \\ \mathbf{v}_2 & = \mathbf{u}_2 -\left( \frac{\mathbf{u}_2 \cdot \mathbf{v}_1}{\mathbf{v}_1 \cdot \mathbf{v}_1}\right) \mathbf{v}_1 \\ \mathbf{v}_3 & = \mathbf{u}_3 -\left( \frac{\mathbf{u}_3 \cdot \mathbf{v}_1}{\mathbf{v}_1 \cdot \mathbf{v}_1}\right) \mathbf{v}_1 -\left( \frac{\mathbf{u}_3 \cdot \mathbf{v}_2}{\mathbf{v}_2 \cdot \mathbf{v}_2}\right) \mathbf{v}_2 \\ &\;\vdots \\ \mathbf{v}_m & = \mathbf{u}_m -\left( \frac{\mathbf{u}_m \cdot \mathbf{v}_1}{\mathbf{v}_1 \cdot \mathbf{v}_1}\right) \mathbf{v}_1 -\left( \frac{\mathbf{u}_m \cdot \mathbf{v}_2}{\mathbf{v}_2 \cdot \mathbf{v}_2}\right) \mathbf{v}_2 -\cdots -\left( \frac{\mathbf{u}_m \cdot \mathbf{v}_{m-1}}{\mathbf{v}_{m-1} \cdot \mathbf{v}_{m-1}}\right) \mathbf{v}_{m-1} \end{aligned}\]

  is an orthogonal basis for \(W_m\)

• An orthonormal basis for \(W_m\) is

  \[B''=\left\{ \mathbf{w}_1, \mathbf{w}_2, \cdots, \mathbf{w}_m \right\}=\left\{ \frac{1}{\left\| \mathbf{v}_1 \right\|} \mathbf{v}_1, \frac{1}{\left\| \mathbf{v}_2 \right\|} \mathbf{v}_2, \cdots, \frac{1}{\left\| \mathbf{v}_m \right\|} \mathbf{v}_m \right\}\]

\(~\)

Example \(\,\)An inner product defined on the vector space \(P_2\) of all polynomials of degree less than or equal to \(2\), is given by

\[\left\langle p, q \right \rangle =\int_{-1}^{1} p(x)\, q(x)\, dx\]

Use the Gram-Schmidt orthogonalization process to transform the given basis for \(P_2\) into an orthogonal basis \(B'\)

\[B = \{1, x, x^2\}\]

\(~\)

Worked Exercises