import numpy as np
from scipy import integrate
import sympy
from sympy import init_printing
init_printing()
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from IPython.display import HTMLAppendix I — Double Pendulum
\(~\)
Consider the rather complicated system of two coupled 2nd-order nonlinear ODEs for a double pendulum
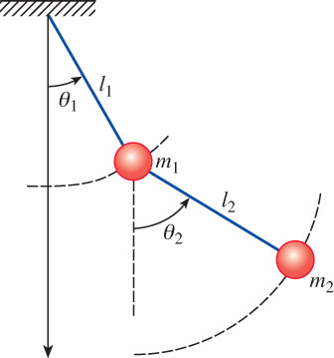
Nonlinear governing equations
\[\scriptsize \begin{aligned} (m_1+m_2) l_1\color{red}{\ddot{\theta_1}} + m_2l_2\color{red}{\ddot{\theta_2}\cos(\theta_1-\theta_2)} & + m_2l_2\color{red}{\left(\dot{\theta_2}\right)^2\sin(\theta_1-\theta_2)}+g(m_1+m_2)\color{red}{\sin(\theta_1)} = 0\\ m_2l_2\color{red}{\ddot{\theta_2}} + m_2l_1\color{red}{\ddot{\theta_1}\cos(\theta_1-\theta_2)} & - m_2l_1 \color{red}{\left(\dot{\theta_1}\right)^2 \sin(\theta_1-\theta_2)} +m_2g\color{red}{\sin(\theta_2)} = 0 \end{aligned}\]
\(~\)
th1, th2 = sympy.symbols("theta_1, theta_2", cls=sympy.Function)
t, g, m1, l1, m2, l2 = sympy.symbols("t, g, m_1, l_1, m_2, l_2")
ode1 = sympy.Eq((m1 +m2) *l1 *th1(t).diff(t, t) +
m2 *l2 *th2(t).diff(t, t) *sympy.cos(th1(t) -th2(t)) +
m2 *l2 *th2(t).diff(t)**2 *sympy.sin(th1(t) -th2(t)) +
g *(m1 +m2) *sympy.sin(th1(t)), 0)
ode2 = sympy.Eq(m2 *l2 *th2(t).diff(t, t) +
m2 *l1 *th1(t).diff(t, t) *sympy.cos(th1(t) -th2(t)) -
m2 *l1 *th1(t).diff(t)**2 *sympy.sin(th1(t) -th2(t)) +
m2 *g *sympy.sin(th2(t)), 0)\(~\)
We first have to write the system of two 2nd-order ODEs as a system of \(\,\)four 1st-order ODEs on standard form. \(\,\)To this end, \(\,\)we need to introduce new functions
\[ \begin{aligned} y_1(t) &= \theta_1(t) \\ y_2(t) &= \dot{\theta_1}(t) \\ y_3(t) &= \theta_2(t) \\ y_4(t) &=\dot{\theta_2}(t) \end{aligned}\]
and rewrite the ODEs in terms of these functions
\(~\)
y1, y2, y3, y4 = sympy.symbols("y_1, y_2, y_3, y_4", cls=sympy.Function)
varchange = {th1(t): y1(t),
th1(t).diff(t, t): y2(t).diff(t),
th2(t): y3(t),
th2(t).diff(t, t): y4(t).diff(t)}
ode1_vc = ode1.subs(varchange)
ode2_vc = ode2.subs(varchange)
ode3 = sympy.Eq(y1(t).diff(t) -y2(t), 0)
ode4 = sympy.Eq(y3(t).diff(t) -y4(t), 0)\(~\)
- At this point, \(\,\)we have four coupled 1st-order ODEs for the functions \(\,y_1\,\) to \(\,y_4\). \(\,\)It only remains to solve for the derivatives of these functions to obtain the ODEs in standard form
\(~\)
y = sympy.Matrix([y1(t), y2(t), y3(t), y4(t)])
vcsol = sympy.solve((ode1_vc, ode2_vc, ode3, ode4), y.diff(t), dict=True)
f = y.diff(t).subs(vcsol[0])
f\(\displaystyle \left[\begin{matrix}y_{2}{\left(t \right)}\\\frac{g m_{1} \sin{\left(y_{1}{\left(t \right)} \right)} + \frac{g m_{2} \sin{\left(y_{1}{\left(t \right)} - 2 y_{3}{\left(t \right)} \right)}}{2} + \frac{g m_{2} \sin{\left(y_{1}{\left(t \right)} \right)}}{2} + \frac{l_{1} m_{2} y_{2}^{2}{\left(t \right)} \sin{\left(2 y_{1}{\left(t \right)} - 2 y_{3}{\left(t \right)} \right)}}{2} + l_{2} m_{2} y_{4}^{2}{\left(t \right)} \sin{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)}}{l_{1} \left(- m_{1} + m_{2} \cos^{2}{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} - m_{2}\right)}\\y_{4}{\left(t \right)}\\\frac{g m_{1} \sin{\left(2 y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} - g m_{1} \sin{\left(y_{3}{\left(t \right)} \right)} + g m_{2} \sin{\left(2 y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} - g m_{2} \sin{\left(y_{3}{\left(t \right)} \right)} + 2 l_{1} m_{1} y_{2}^{2}{\left(t \right)} \sin{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} + 2 l_{1} m_{2} y_{2}^{2}{\left(t \right)} \sin{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} + l_{2} m_{2} y_{4}^{2}{\left(t \right)} \sin{\left(2 y_{1}{\left(t \right)} - 2 y_{3}{\left(t \right)} \right)}}{2 l_{2} \left(m_{1} - m_{2} \cos^{2}{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} + m_{2}\right)}\end{matrix}\right]\)
jac = sympy.Matrix([[f_i.diff(y_j) for y_j in y] for f_i in f])
jac[:, 0]\(\displaystyle \left[\begin{matrix}0\\\frac{2 m_{2} \left(g m_{1} \sin{\left(y_{1}{\left(t \right)} \right)} + \frac{g m_{2} \sin{\left(y_{1}{\left(t \right)} - 2 y_{3}{\left(t \right)} \right)}}{2} + \frac{g m_{2} \sin{\left(y_{1}{\left(t \right)} \right)}}{2} + \frac{l_{1} m_{2} y_{2}^{2}{\left(t \right)} \sin{\left(2 y_{1}{\left(t \right)} - 2 y_{3}{\left(t \right)} \right)}}{2} + l_{2} m_{2} y_{4}^{2}{\left(t \right)} \sin{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)}\right) \sin{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} \cos{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)}}{l_{1} \left(- m_{1} + m_{2} \cos^{2}{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} - m_{2}\right)^{2}} + \frac{g m_{1} \cos{\left(y_{1}{\left(t \right)} \right)} + \frac{g m_{2} \cos{\left(y_{1}{\left(t \right)} - 2 y_{3}{\left(t \right)} \right)}}{2} + \frac{g m_{2} \cos{\left(y_{1}{\left(t \right)} \right)}}{2} + l_{1} m_{2} y_{2}^{2}{\left(t \right)} \cos{\left(2 y_{1}{\left(t \right)} - 2 y_{3}{\left(t \right)} \right)} + l_{2} m_{2} y_{4}^{2}{\left(t \right)} \cos{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)}}{l_{1} \left(- m_{1} + m_{2} \cos^{2}{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} - m_{2}\right)}\\0\\- \frac{m_{2} \left(g m_{1} \sin{\left(2 y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} - g m_{1} \sin{\left(y_{3}{\left(t \right)} \right)} + g m_{2} \sin{\left(2 y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} - g m_{2} \sin{\left(y_{3}{\left(t \right)} \right)} + 2 l_{1} m_{1} y_{2}^{2}{\left(t \right)} \sin{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} + 2 l_{1} m_{2} y_{2}^{2}{\left(t \right)} \sin{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} + l_{2} m_{2} y_{4}^{2}{\left(t \right)} \sin{\left(2 y_{1}{\left(t \right)} - 2 y_{3}{\left(t \right)} \right)}\right) \sin{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} \cos{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)}}{l_{2} \left(m_{1} - m_{2} \cos^{2}{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} + m_{2}\right)^{2}} + \frac{2 g m_{1} \cos{\left(2 y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} + 2 g m_{2} \cos{\left(2 y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} + 2 l_{1} m_{1} y_{2}^{2}{\left(t \right)} \cos{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} + 2 l_{1} m_{2} y_{2}^{2}{\left(t \right)} \cos{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} + 2 l_{2} m_{2} y_{4}^{2}{\left(t \right)} \cos{\left(2 y_{1}{\left(t \right)} - 2 y_{3}{\left(t \right)} \right)}}{2 l_{2} \left(m_{1} - m_{2} \cos^{2}{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} + m_{2}\right)}\end{matrix}\right]\)
jac[:, 1]\(\displaystyle \left[\begin{matrix}1\\\frac{m_{2} y_{2}{\left(t \right)} \sin{\left(2 y_{1}{\left(t \right)} - 2 y_{3}{\left(t \right)} \right)}}{- m_{1} + m_{2} \cos^{2}{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} - m_{2}}\\0\\\frac{4 l_{1} m_{1} y_{2}{\left(t \right)} \sin{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} + 4 l_{1} m_{2} y_{2}{\left(t \right)} \sin{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)}}{2 l_{2} \left(m_{1} - m_{2} \cos^{2}{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} + m_{2}\right)}\end{matrix}\right]\)
jac[:, 2]\(\displaystyle \left[\begin{matrix}0\\- \frac{2 m_{2} \left(g m_{1} \sin{\left(y_{1}{\left(t \right)} \right)} + \frac{g m_{2} \sin{\left(y_{1}{\left(t \right)} - 2 y_{3}{\left(t \right)} \right)}}{2} + \frac{g m_{2} \sin{\left(y_{1}{\left(t \right)} \right)}}{2} + \frac{l_{1} m_{2} y_{2}^{2}{\left(t \right)} \sin{\left(2 y_{1}{\left(t \right)} - 2 y_{3}{\left(t \right)} \right)}}{2} + l_{2} m_{2} y_{4}^{2}{\left(t \right)} \sin{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)}\right) \sin{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} \cos{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)}}{l_{1} \left(- m_{1} + m_{2} \cos^{2}{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} - m_{2}\right)^{2}} + \frac{- g m_{2} \cos{\left(y_{1}{\left(t \right)} - 2 y_{3}{\left(t \right)} \right)} - l_{1} m_{2} y_{2}^{2}{\left(t \right)} \cos{\left(2 y_{1}{\left(t \right)} - 2 y_{3}{\left(t \right)} \right)} - l_{2} m_{2} y_{4}^{2}{\left(t \right)} \cos{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)}}{l_{1} \left(- m_{1} + m_{2} \cos^{2}{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} - m_{2}\right)}\\0\\\frac{m_{2} \left(g m_{1} \sin{\left(2 y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} - g m_{1} \sin{\left(y_{3}{\left(t \right)} \right)} + g m_{2} \sin{\left(2 y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} - g m_{2} \sin{\left(y_{3}{\left(t \right)} \right)} + 2 l_{1} m_{1} y_{2}^{2}{\left(t \right)} \sin{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} + 2 l_{1} m_{2} y_{2}^{2}{\left(t \right)} \sin{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} + l_{2} m_{2} y_{4}^{2}{\left(t \right)} \sin{\left(2 y_{1}{\left(t \right)} - 2 y_{3}{\left(t \right)} \right)}\right) \sin{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} \cos{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)}}{l_{2} \left(m_{1} - m_{2} \cos^{2}{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} + m_{2}\right)^{2}} + \frac{- g m_{1} \cos{\left(2 y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} - g m_{1} \cos{\left(y_{3}{\left(t \right)} \right)} - g m_{2} \cos{\left(2 y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} - g m_{2} \cos{\left(y_{3}{\left(t \right)} \right)} - 2 l_{1} m_{1} y_{2}^{2}{\left(t \right)} \cos{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} - 2 l_{1} m_{2} y_{2}^{2}{\left(t \right)} \cos{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} - 2 l_{2} m_{2} y_{4}^{2}{\left(t \right)} \cos{\left(2 y_{1}{\left(t \right)} - 2 y_{3}{\left(t \right)} \right)}}{2 l_{2} \left(m_{1} - m_{2} \cos^{2}{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} + m_{2}\right)}\end{matrix}\right]\)
jac[:, 3]\(\displaystyle \left[\begin{matrix}0\\\frac{2 l_{2} m_{2} y_{4}{\left(t \right)} \sin{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)}}{l_{1} \left(- m_{1} + m_{2} \cos^{2}{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} - m_{2}\right)}\\1\\\frac{m_{2} y_{4}{\left(t \right)} \sin{\left(2 y_{1}{\left(t \right)} - 2 y_{3}{\left(t \right)} \right)}}{m_{1} - m_{2} \cos^{2}{\left(y_{1}{\left(t \right)} - y_{3}{\left(t \right)} \right)} + m_{2}}\end{matrix}\right]\)
params = {m1: 5.0, l1: 2.0, m2: 5.0, l2: 1.0, g: 9.8}
f_np = sympy.lambdify((t, y), f.subs(params), 'numpy')
jac_np = sympy.lambdify((t, y), jac.subs(params), 'numpy')y0 = [2.0, 0.0, 0.0, 0.0]
t = np.linspace(0, 20, 1000)
r = integrate.ode(f_np, jac_np).set_initial_value(y0, t[0])dt = t[1] - t[0]
y = np.zeros((len(t), len(y0)))
idx = 0
while r.successful() and r.t < t[-1]:
y[idx, :] = r.y
r.integrate(r.t + dt)
idx += 1\(~\)
- When visualizing this solution, \(\,\)it is more intuitive to animate the positions of the pendulums in the \(\,x–y\,\) plane rather than their angular deflections
\(~\)
th1_np, th2_np = y[:, 0], y[:, 2]
x1 = params[l1] *np.sin(th1_np)
y1 = -params[l1] *np.cos(th1_np)
x2 = x1 +params[l2] *np.sin(th2_np)
y2 = y1 -params[l2] *np.cos(th2_np)fig, ax = plt.subplots(figsize=(6, 6))
ax.set_xlabel('$x$', fontsize=16)
ax.set_ylabel('$y$', fontsize=16)
ax.set_xticks([-4, -2, 0, 2, 4])
ax.set_yticks([-4, -2, 0, 2, 4])
ax.set_xticklabels([-4, -2, 0, 2, 4], fontsize=14)
ax.set_yticklabels([-4, -2, 0, 2, 4], fontsize=14)
ax.set_xlim(-4, 4)
ax.set_ylim(-4, 4)
ax.tick_params(which='both', direction='in')
plt.close()line1, = ax.plot([], [], 'o-', color='r', markersize=4.0, lw=2)
line2, = ax.plot([], [], 'o-', color='b', markersize=20.0, lw=2)
time_text = ax.text(0.05, 0.9, '', fontsize=18, transform=ax.transAxes)
def init():
line1.set_data([], [])
line2.set_data([], [])
time_text.set_text('')
return line1, line2, time_text
def animate(i):
t_x1 = [0, x1[i]]
t_y1 = [0, y1[i]]
t_x2 = [x1[i], x2[i]]
t_y2 = [y1[i], y2[i]]
line1.set_data(t_x1, t_y1)
line2.set_data(t_x2, t_y2)
time_text.set_text(f'time = {i*dt:.1f}s')
return line1, line2, time_text
anim = FuncAnimation(fig, animate, range(1, len(y)),
interval=dt*1000, blit=True, init_func=init)
HTML('<center>' + anim.to_html5_video() + '</center>')