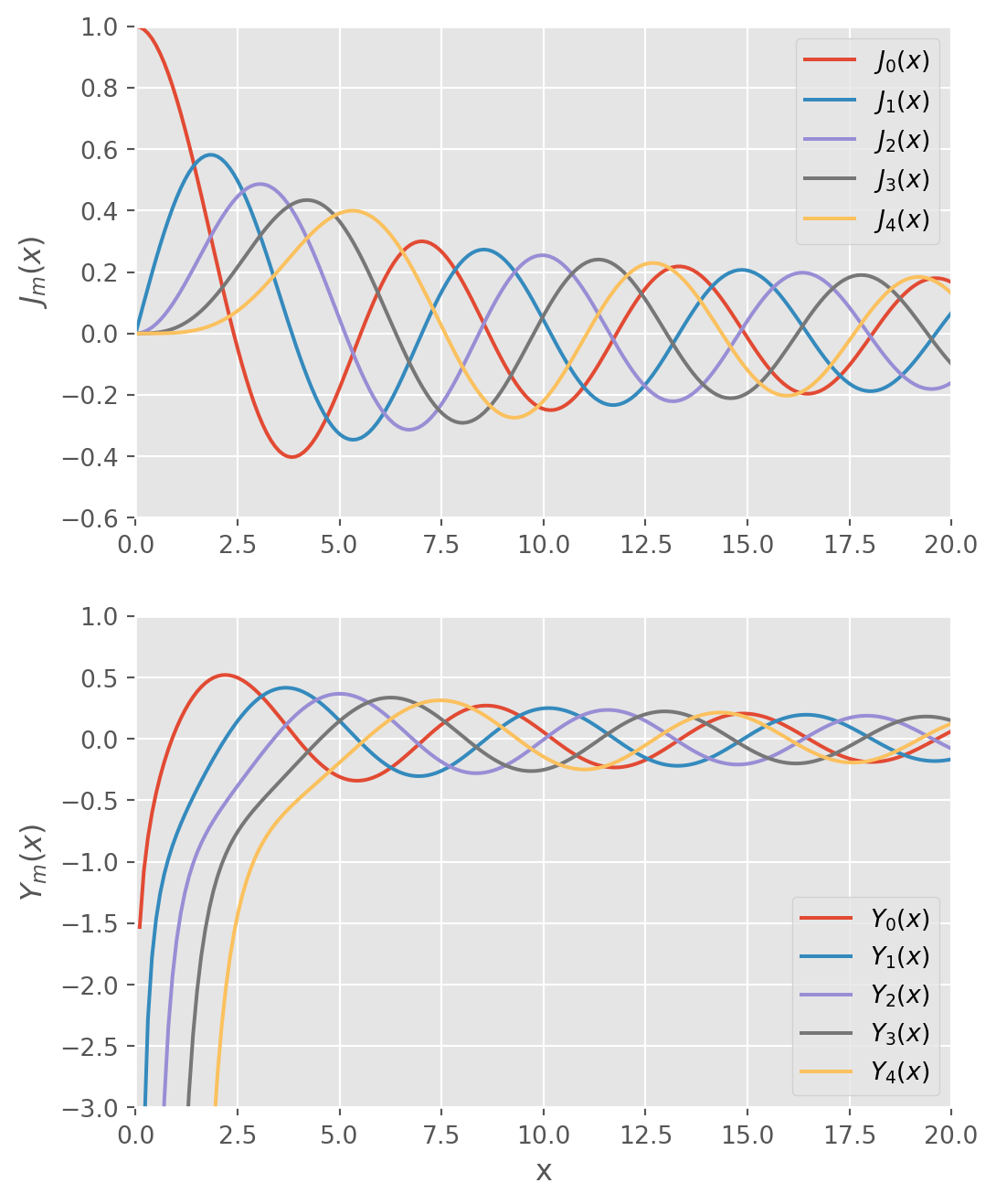
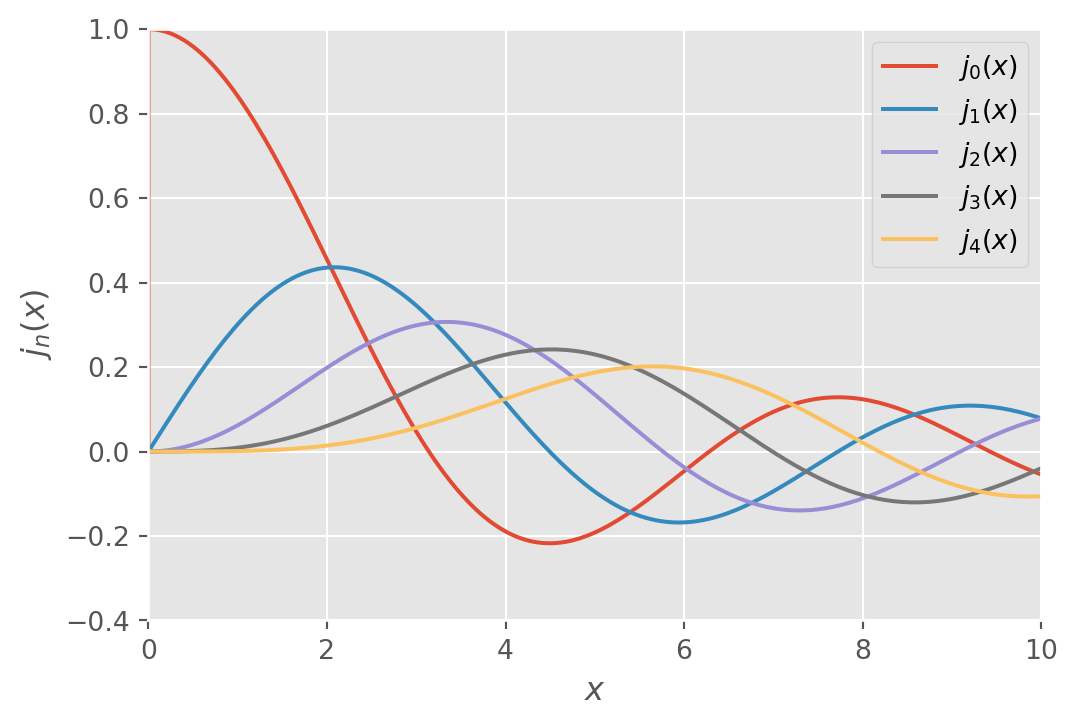
Worked Exercises
1. \(\phantom{1}\) The differential equation
\[ xy'' +(1-x) y' +\alpha y=0\]
\(~\) is known as Laguerre’s equation
(a)\(~\) Find two linearly independent solutions for \(0 \le x <\infty\)
(b)\(~\) Show that there is a polynomial solution of degree \(n\), in case \(\alpha=n\) is a non-negative integer
(c)\(~\) These solutions are naturally called Laguerre polynomials and are denoted by \(L_n(x)\). Rodrigues’ formula for the Laguerre polynomials is
\[ L_n(x) = \frac{e^x}{n!} \frac{d^n}{dx^n} x^n e^{-x}\]
Use this formula to find the Laguerre polynomials corresponding to \(n=0,1,2,3,4\)
\(~\)
Solution (a)
Let’s apply the Frobenius method to solve the differential equation near the regular singular point at \(x = 0\)
Step 1: Frobenius Series Assumption
Assume a solution of the form:
\[ \color{blue}{y(x) = x^r \sum_{k=0}^{\infty} a_k x^k = \sum_{k=0}^{\infty} a_k x^{k + r}, \quad a_0 \ne 0}\]
Then,
\[ y'(x) = \sum_{k=0}^{\infty} a_k (k + r) x^{k + r - 1}\]
\[
y''(x) = \sum_{k=0}^{\infty} a_k (k + r)(k + r - 1) x^{k + r - 2}\]
Step 2: Substitute into the Equation
Substitute into the original equation:
\[\scriptsize\begin{aligned}
& x y'' + (1 - x) y' + n y \\
&= \sum_{k=0}^{\infty} a_k (k + r)(k + r - 1) x^{k + r - 1}
+\sum_{k=0}^{\infty} a_k (k + r) x^{k + r - 1}
-\sum_{k=0}^{\infty} a_k (k + r) x^{k + r}
+\sum_{k=0}^{\infty} \alpha a_k x^{k + r} = 0
\end{aligned}\]
Group and simplify:
\[
\sum_{k=0}^{\infty} a_k (k + r)^2 x^{k + r - 1}
+\sum_{k=0}^{\infty} a_k (\alpha - k - r) x^{k + r} = 0
\]
Step 3: Indicial Equation
The lowest power of \(x\) is \(x^{r - 1}\). Its coefficient is:
\[
a_0 r^2\]
Set this to zero:
\[
\color{blue}{r^2 = 0 \quad \Rightarrow \quad r = 0}\]
Step 4: Recurrence Relation
Now use \(r = 0\), so:
\[ \sum_{k=0}^{\infty} \left[ a_{k+1} (k + 1)^2 + a_k (\alpha - k) \right] x^k = 0\]
So the recurrence relation is:
\[ \color{blue}{a_{k+1} = - \frac{(\alpha - k)}{(k + 1)^2} a_k}\]
Choose \(a_0 = 1\) (arbitrary constant), this gives a general form:
\[\color{blue}{a_k = \frac{(-1)^k \alpha(\alpha - 1) \cdots (\alpha - k + 1)}{(k!)^2}}
\]
Thus the first solution is
\[ \color{blue}{y_1(x) = \sum_{k=0}^{\infty} a_k x^k}\]
When the indicial equation has a repeated root \(r=0\), the second solution has the form:
\[ \color{blue}{y_2(x) = y_1(x) \ln x + \sum_{k=0}^{\infty} b_k x^k}\]
We plug this into the original equation. This leads to
\[ 2y_1' -y_1 +\sum_{k=0}^\infty \left[ (k+1)^2 b_{k+1} +(\alpha -k) b_k \right] x^k = 0\]
Solution (b)
When \(\alpha = n\),
\[
a_k = \frac{(-1)^k n!}{(n - k)! (k!)^2}
\quad \text{for } k \le n\]
For \(k > n\), we get \(a_k = 0\), so the series terminates. The series becomes a polynomial of degree \(n\):
\[\color{blue}{y_1(x) = \sum_{k=0}^{n} \frac{(-1)^k n!}{(n - k)! (k!)^2} x^k = L_n(x)}\]
The second linearly independent solution is of the form:
\[ y_2(x) = L_n(x) \ln x + \sum_{k=0}^{\infty} d_k x^k\]
Solution (c)
To find the Laguerre polynomials \(L_n(x)\) for \(n = 0, 1, 2, 3, 4\), we will use Rodrigues’ formula.
\[\color{blue}{L_0(x) = \frac{e^x}{0!} \frac{d^0}{dx^0} \left( x^0 e^{-x} \right) = e^x \cdot e^{-x} = 1}\]
\[ \color{blue}{L_1(x) = \frac{e^x}{1!} \frac{d}{dx} \left( x e^{-x} \right) = e^x \cdot (1 - x) e^{-x} = 1 - x}\]
\[ \color{blue}{L_2(x) = \frac{e^x}{2!} \frac{d^2}{dx^2} \left( x^2 e^{-x} \right) = 1 - 2x + \frac{1}{2}x^2}\]
\[\color{blue}{L_3(x) = 1 - 3x + \frac{3}{2}x^2 - \frac{1}{6}x^3}\]
\[ \color{blue}{ L_4(x) = 1 - 4x + 3x^2 - \frac{2}{3}x^3 + \frac{1}{24}x^4}\]
\(~\)
2. \(\phantom{1}\) The differential equation
\[ (1 -x^2) y'' -xy' +\alpha^2 y=0\]
\(~\) where \(\alpha\) is a parameter, is known as Chebyshev’s equation
(a)\(~\) Find two power series solutions centered at the ordinary point \(0\)
(b)\(~\) When \(\alpha=n\) is a nonnegative integer, show that Chebyshev’s differential equation always possesses a polynomial solution of degree \(n\)
(c)\(~\) These solutions are naturally called Chebyshev polynomials and are denoted by \(T_n(x)\). Rodrigues’ formula for the Chebyshev polynomials is
\[T_n(x) = (-1)^n \frac{2^n n!}{(2n)!} \sqrt{1-x^2}\frac{d^n}{dx^n} (1-x^2)^{n-1/2}\]
Use this formula to find the Chebyshev polynomials corresponding to \(n=0,1,2,3\)
\(~\)
Solution (a)
We are to find two linearly independent power series solutions centered at \(x = 0\), which is an ordinary point (i.e., the coefficients of \(y''\) and \(y'\) are analytic at \(x = 0\))
Step 1: Assume a Power Series Solution
Let’s assume a solution of the form:
\[\color{blue}{y(x) = \sum_{k=0}^{\infty} a_k x^k}\]
Then compute the derivatives:
\[y'(x) = \sum_{k=1}^{\infty} k a_k x^{k-1}, \quad
y''(x) = \sum_{k=2}^{\infty} k(k-1) a_k x^{k-2}\]
Now substitute \(y, y', y''\) into the differential equation:
\[\scriptsize\sum_{k=2}^{\infty} k(k-1) a_k x^{k-2}
-\sum_{k=2}^{\infty} k(k-1) a_k x^k
-\sum_{k=1}^{\infty} k a_k x^k
+\sum_{k=0}^{\infty} \alpha^2 a_k x^k = 0\]
Shift the first term to match powers of \(x^k\) and combine all terms and simplify the coefficients:
\[\color{blue}{\sum_{k=0}^{\infty} \left[
(k+2)(k+1) a_{k+2}
+(\alpha^2 - k^2) a_k
\right] x^k = 0}\]
Set each coefficient of \(x^k\) to \(0\), we get the recurrence relation:
\[
\color{blue}{a_{k+2} = -\frac{\alpha^2 - k^2}{(k+2)(k+1)} a_k}\]
Step 2: Build Two Linearly Independent Solutions
We choose \(a_0\) and \(a_1\) arbitrarily to construct two independent solutions
First solution: even powers only (let \(a_0 = 1\), \(a_1 = 0\))
Then the series becomes:
\[y_1(x) = a_0 + a_2 x^2 + a_4 x^4 + \cdots\]
Use recurrence:
\[a_2 = -\frac{\alpha^2 - 0^2}{2 \cdot 1} a_0 = -\frac{\alpha^2}{2}\]
\[a_4 = -\frac{\alpha^2 - 2^2}{4 \cdot 3} a_2 = -\frac{\alpha^2 - 4}{12} a_2 = \frac{(\alpha^2 - 4)(\alpha^2)}{24}\]
And so on
Second solution: odd powers only (let \(a_0 = 0\), \(a_1 = 1\))
Then the series becomes:
\[y_2(x) = a_1 x + a_3 x^3 + a_5 x^5 + \cdots\]
Use recurrence:
\[a_3 = -\frac{\alpha^2 - 1^2}{3 \cdot 2} a_1 = -\frac{\alpha^2 - 1}{6}\]
\[a_5 = -\frac{\alpha^2 - 3^2}{5 \cdot 4} a_3 = \frac{(\alpha^2 - 9)(\alpha^2 - 1)}{120}\]
And so on
Two linearly independent power series solutions centered at \(x = 0\) are:
\[
\color{blue}{y_1(x) = a_0 \left[ 1 - \frac{\alpha^2}{2} x^2 + \frac{(\alpha^2 - 4)\alpha^2}{24} x^4 - \cdots \right]}
\]
\[
\color{blue}{y_2(x) = a_1 \left[ x - \frac{\alpha^2 - 1}{6} x^3 + \frac{(\alpha^2 - 1)(\alpha^2 - 9)}{120} x^5 - \cdots \right]}
\]
Solution (b)
Let \(\alpha = n\), a nonnegative integer. Then the recurrence becomes:
\[ a_{k+2} = -\frac{n^2 - k^2}{(k+2)(k+1)} a_k\]
Observe that when \(\color{blue}{k = n}\), we get:
\[ \color{blue}{a_{n+2} = -\frac{n^2 - n^2}{(n+2)(n+1)} a_n = 0}\]
If we start with \(a_0 \ne 0\), and define the even-power solution:
\[\color{red}{y(x) = a_0 + a_2 x^2 + a_4 x^4 + \cdots}\]
then for even \(n\), the recurrence will produce:
\[\color{red}{a_{n+2} = 0 \Rightarrow \text{ the series terminates at } x^n}\]
So, the solution is a polynomial of degree \(n\)
Similarly, if \(a_1 \ne 0\), the odd-power series will terminate at \(x^n\) when \(n\) is odd. Thus, we get a polynomial solution of degree exactly \(n\)
These solutions are known as the Chebyshev polynomials of the first kind, usually denoted \(T_n(x).\) However the recurrence continues — unless we start with initial coefficients \(a_0\), \(a_1\) that make the series terminate
Solution (c)
Let’s define:
\[ f_n(x) = (1 - x^2)^{n - \frac{1}{2}}, \quad \text{then} \quad T_n(x) = (-1)^n \frac{2^n n!}{(2n)!} \sqrt{1 - x^2} \cdot \frac{d^n}{dx^n} f_n(x)\]
\(n = 0\)
We have: \(\displaystyle f_0(x) = (1 - x^2)^{-1/2}, \quad \text{but} \quad \frac{d^0}{dx^0} f_0 = f_0\)
\(\color{red}{T_0(x) = \frac{1}{1} \cdot \sqrt{1 - x^2} \cdot (1 - x^2)^{-1/2} = 1}\)
\(n = 1\)
\(f_1(x) = (1 - x^2)^{1 - \frac{1}{2}} = (1 - x^2)^{1/2}\)
Differentiate:
\(\displaystyle \frac{d}{dx} (1 - x^2)^{1/2} = \frac{1}{2}(1 - x^2)^{-1/2} \cdot (-2x) = -\frac{x}{\sqrt{1 - x^2}}\)
Now plug into the formula:
\(\displaystyle \color{red}{T_1(x)} = (-1)^1 \cdot \frac{2^1 \cdot 1!}{2!} \cdot \sqrt{1 - x^2} \cdot \left( -\frac{x}{\sqrt{1 - x^2}} \right) = x\)
\(n = 2\)
\(f_2(x) = (1 - x^2)^{3/2}\)
Differentiate twice:
First derivative:
\(f_2'(x) = \frac{3}{2}(1 - x^2)^{1/2} \cdot (-2x) = -3x (1 - x^2)^{1/2}\)
Second derivative:
\(f_2''(x) = \frac{d}{dx} [-3x (1 - x^2)^{1/2}]
= -3(1 - x^2)^{1/2} + 3x^2 (1 - x^2)^{-1/2}\)
Now plug into Rodrigues’ formula:
\(\color{red}{
\begin{aligned}
T_2(x) &= \frac{2^2 \cdot 2!}{(4)!} \cdot \sqrt{1 - x^2} \cdot f_2''(x) \\
&= {\scriptsize\frac{4 \cdot 2}{24} \cdot \sqrt{1 - x^2} \cdot \left[ -3(1 - x^2)^{1/2} + 3x^2(1 - x^2)^{-1/2} \right]} \\
&= 2x^2 - 1
\end{aligned}}\)
\(n = 3\)
\(f_3(x) = (1 - x^2)^{5/2}\)
We’ll compute the 3rd derivative and plug it into the formula:
\(\color{red}{
\begin{aligned}
T_3(x) &= (-1)^3 \cdot \frac{2^3 \cdot 3!}{(6)!} \cdot \sqrt{1 - x^2} \cdot f_3’’’(x)\\
&= {\scriptsize-\frac{8 \cdot 6}{720} \cdot \sqrt{1 - x^2} \cdot \left[ 45x(1 - x^2)^{1/2} - 15x^3 (1 - x^2)^{-1/2} \right]}\\
&= 4x^3 - 3x
\end{aligned}}\)
\(~\)
3. \(~\) If \(n\) is an integer, you can use the substitution \(R(x)=(\alpha x)^{-1/2} \, Z(x)\) to solve that the differential equation
\[ x^2 \frac{d^2R}{dx^2} +2x \frac{dR}{dx} +\left[ \alpha^2 x^2 - n(n+1) \right] R = 0 \]
Find the general solution of the differential equation on the interval \((0, \infty)\)
Solution
Step 1: \(~\) Apply the substitution
Let:
\[R(x) = (\alpha x)^{-1/2} Z(x) = \frac{1}{\sqrt{\alpha x}} Z(x)\]
We compute derivatives of \(R(x)\):
First derivative:
Using the product rule:
\[\frac{dR}{dx} = \frac{d}{dx} \left( \frac{1}{\sqrt{\alpha x}} Z(x) \right)
= \frac{d}{dx} \left( \alpha^{-1/2} x^{-1/2} Z(x) \right)\]
Now differentiate:
\[\frac{dR}{dx} = \alpha^{-1/2} \left( -\frac{1}{2} x^{-3/2} Z(x) + x^{-1/2} Z’(x) \right)\]
Second derivative:
Differentiate again:
\[\frac{d^2R}{dx^2} = \alpha^{-1/2}
\left[ \frac{3}{4} x^{-5/2} Z(x) - x^{-3/2} Z’(x) + x^{-1/2} Z’’(x) \right]\]
Step 2: \(~\) Plug into the original equation
Now substitute \(R\), \(R'\), \(R''\) into the equation:
\[x^2 R'' + 2x R' + \left( \alpha^2 x^2 - n(n+1) \right) R = 0\]
Thus the equation becomes:
\[\alpha^{-1/2} \left[ x^{3/2} Z'' + x^{1/2} Z' + \left( \alpha^2 x^{3/2} - \left(n(n+1) + \frac{1}{4} \right) x^{-1/2} \right) Z \right] = 0\]
Factor out \(x^{1/2}\):
\[\alpha^{-1/2} x^{1/2} \left[
x Z'' + Z' + \left( \alpha^2 x - \frac{n(n+1) + \tfrac{1}{4}}{x} \right) Z
\right] = 0\]
So the reduced equation is:
\[x Z'' + Z' + \left( \alpha^2 x - \frac{n(n+1) + \tfrac{1}{4}}{x} \right) Z = 0\]
Step 3: \(~\) Change variable to standard form
Let’s define:
\[u = \alpha x
\;\Rightarrow\;
\frac{dZ}{dx} = \alpha \frac{dZ}{du}, \quad \frac{d^2Z}{dx^2} = \alpha^2 \frac{d^2Z}{du^2}\]
Plug into the reduced equation and simplify:
\[u Z'' + Z' + \left( u - \frac{n(n+1) + \frac{1}{4}}{u} \right) Z = 0\]
Now multiply through by \(u\):
\[u^2 Z'' + u Z' + \left( u^2 - \left(n(n+1) + \tfrac{1}{4} \right) \right) Z = 0\]
Step 4: \(~\) Identify the equation
This is Bessel’s equation of order \(\nu\), where:
\[\nu^2 = n(n+1) + \tfrac{1}{4}
\;\Rightarrow\;
\nu = \sqrt{n(n+1) + \tfrac{1}{4}} = n + \tfrac{1}{2}\]
(because \(n\) is an integer, and this square root simplifies nicely)
So we now recognize:
\[u^2 Z'' + u Z' + (u^2 - (n + \tfrac{1}{2})^2) Z = 0\]
Final Answer
The general solution is:
\[R(x) = \frac{1}{\sqrt{\alpha x}} \left[ A J_{n + 1/2} (\alpha x) + B Y_{n + 1/2} (\alpha x) \right]\]
\(~\)
4. \(~\) Use the indicated change of variable to find the general solution of the given differential equation on the interval \((0, \infty)\)
\[ x^2 y'' +\left( \alpha^2 x^2 - \nu^2 +\frac{1}{4} \right)y = 0, \;\;y= \sqrt{x} \,u(x)\]
Solution
Step 1: \(~\) Compute derivatives of \(y = \sqrt{x} u(x)\)
\[y' = \frac{1}{2} x^{-1/2} u(x) + x^{1/2} u'(x)\]
\[y'' = -\frac{1}{4} x^{-3/2} u(x) + x^{-1/2} u'(x) + x^{1/2} u''(x)\]
Step 2: \(~\) Plug into the original equation
Now the full equation becomes:
\[\left( -\frac{1}{4} x^{1/2} u + x^{3/2} u' + x^{5/2} u'' \right)
+ \left( \alpha^2 x^2 - \nu^2 + \frac{1}{4} \right) x^{1/2} u = 0\]
Group like terms and factor out \(x^{1/2}\):
\[x^{1/2} \left( x^2 u'' + x u' + (\alpha^2 x^2 - \nu^2) u \right) = 0\]
Since \(x^{1/2} > 0\) on \((0, \infty)\), we divide both sides:
\[x^2 u'' + x u' + (\alpha^2 x^2 - \nu^2) u = 0\]
This is a parameterized Bessel differential equation
Final Answer
The general solution is:
\[y(x) = \sqrt{x} \left[ A J_\nu(\alpha x) + B Y_\nu(\alpha x) \right]\]
\(~\)
5. \(~\) When \(n=0\), Legendre’s differential equation has the polynomial solution \(y=P_0(x)=1\). Use reduction of order to find a second Legendre function satisfying the DE on the interval \((-1,1)\)
Solution
Step 1: \(~\)Use reduction of order
Let:
\[y_2(x) = v(x) y_1(x) = v(x) \cdot 1 = v(x)\]
So we’re seeking a second solution \(y_2(x) = v(x)\), where \(y_1(x) = 1\) is a known solution
Step 2: \(~\) Plug into the equation
Start from the reduced equation:
\[(1 - x^2) y'' - 2x y' = 0\]
Since \(y = v(x)\), we compute:
\[y' = v', \quad y'' = v''\]
So the equation becomes:
\[(1 - x^2) v'' - 2x v' = 0\]
This is a first-order ODE in \(v'\) if we let \(w = v'\). Then:
\[(1 - x^2) w' - 2x w = 0
\quad \text{(a linear first-order equation in \( w \))}\]
Step 3: \(~\) Solve for \(w\)
We rewrite the equation as:
\[w' - \frac{2x}{1 - x^2} w = 0\]
This is a linear first-order ODE. Use integrating factor:
\[\mu(x) = \exp\left( -\int \frac{2x}{1 - x^2} dx \right)\]
Let \(u = 1 - x^2 \Rightarrow du = -2x dx\)
Then:
\[\int \frac{2x}{1 - x^2} dx = -\int \frac{1}{u} du = -\ln|1 - x^2|\]
So:
\[\mu(x) = e^{\ln|1 - x^2|} = |1 - x^2|\]
but on \((-1, 1)\), \(1 - x^2 > 0\) so:,
\[\mu(x) = 1 - x^2\]$$
Now solve:
\[\frac{d}{dx}(w \cdot \mu(x)) = 0
\Rightarrow w(1 - x^2) = C
\Rightarrow w = \frac{C}{1 - x^2}\]
Recall \(w = v'\), so:
\[v’ = \frac{C}{1 - x^2}
\Rightarrow v(x) = C \int \frac{1}{1 - x^2} dx\]
So:
\[v(x) = \frac{C}{2} \ln\left| \frac{1 + x}{1 - x} \right| + D\]
Step 4: \(~\) General solution
We already had \(y_1(x) = 1\), and now we have:
\[y_2(x) = v(x) = \frac{1}{2} \ln\left( \frac{1 + x}{1 - x} \right)
\quad \text{(valid on } (-1,1) \text{ where the log is real)}\]
\(~\)
6. \(~\) When \(n=1\), Legendre’s differential equation has the polynomial solution \(y=P_1(x)=x\). Use reduction of order to find a second Legendre function satisfying the DE on the interval \((-1,1)\)
Solution
Step 1: \(~\) Use reduction of order
Let:
\[y_2(x) = v(x) \cdot y_1(x) = v(x) \cdot x\]
Plug into the differential equation:
\[(1 - x^2)(v''x + 2v') - 2x(v'x + v) + 2(vx) = 0\]
Expand and simplify:
\[x(1 - x^2)v'' + (2 - 4x^2)v' = 0\]
Step 2: \(~\) Let \(w = v'\), then solve
Let \(w = v'\), so \(w' = v''\). Then:
\[x(1 - x^2) w' + (2 - 4x^2) w = 0\]
We rewrite as:
\[w' + \frac{2 - 4x^2}{x(1 - x^2)} w = 0\]
Step 3: \(~\) Solve a first-order linear ODE
Integrating factor:
\[\scriptsize\mu(x) = \exp\left( \int \frac{2 - 4x^2}{x(1 - x^2)} dx \right) = \exp \left( \int \left( \frac{2}{x} - \frac{1}{1 - x} + \frac{1}{1 + x} \right) dx \right)
= x^2 \cdot \frac{1}{1 - x} \cdot (1 + x)
\]
Now solve the equation:
\[\frac{d}{dx} \left( w \cdot \mu(x) \right) = 0 \Rightarrow w \cdot \mu(x) = C \Rightarrow w = \frac{C}{\mu(x)} = C \cdot \frac{1 - x}{x^2(1 + x)}\]
Now integrate to find \(v\):
\[\begin{aligned}
v &= \int w \, dx = C \int \frac{1 - x}{x^2(1 + x)} dx\\
&= C \int \left( \frac{1}{x^2} - \frac{2}{x} + \frac{2}{1 + x} \right) dx \\
&= C \left( -\frac{1}{x} - 2\ln|x| + 2\ln|1 + x| \right) + D
\end{aligned}\]
Final Answer:
The second linearly independent solution for \(n = 1\) on \((-1, 1)\) is:
\[
y_2(x) = -1 - 2x \ln|x| + 2x \ln|1 + x|
\quad \text{(up to constant multiples)}\]
