Appendix K — The FEniCS computing platform

FEniCS is a popular open-source computing platform for solving partial differential equations (PDEs) with the finite element method (FEM). FEniCS enables users to quickly translate scientific models into efficient finite element code. With the high-level Python and C++ interfaces to FEniCS, it is easy to get started, but FEniCS offers also powerful capabilities for more experienced programmers. FEniCS runs on a multitude of platforms ranging from laptops to high-performance computers

K.1 Getting started

The latest stable release of FEniCSx is version 0.9, which was released in October 2024. The easiest way to start using FEniCSx on MacOS and other systems is to install it using conda:

$ conda create -n fenicsx
$ conda activate fenicsx
$ conda install -c conda-forge fenics-dolfinx mpich pyvista 
$ conda install -c conda-forge petsc petsc4py
$ conda install ipykernel
$ python -m ipykernel install \
>       --user --name fenicsx --display-name "FEniCSx"
import dolfinx
print(f'DOLFINx version: {dolfinx.__version__}')
DOLFINx version: 0.9.0

K.2 An Overview of the FEniCS Project

  • The FEniCS Project is a research and software initiative focused on developing mathematical methods and software for solving partial differential equations (PDEs). Its goal is to provide intuitive, efficient, and flexible tools for scientific computing. Launched in 2003, the project is the result of collaboration among researchers from universities and research institutes worldwide. For the latest updates and more information, visit the FEniCS Project

  • The latest version of the FEniCS project, FEniCSx, consists of several building blocks, namely DOLFINx, UFL, FFCx, and Basix. We will now go through the main objectives of each of these building blocks

    • DOLFINx is the high performance C++ backend of FEniCSx, where structures such as meshes, function spaces and functions are implemented. Additionally, DOLFINx also contains compute intensive functions such as finite element assembly and mesh refinement algorithms. It also provides an interface to linear algebra solvers and data-structures, such as PETSc
    • UFL is a high-level form language for describing variational formulations with a high-level mathematical syntax
    • FFCx is the form compiler of FEniCSx; given variational formulations written with UFL, it generates efficient C code
    • Basix is the finite element backend of FEniCSx, responsible for generating finite element basis functions

K.3 What you will learn

The goal of this tutorial is to demonstrate how to apply the finite element to solve PDEs using FEniCS. Through a series of examples, we will demonstrate how to:

  • Solve linear PDEs (such as the Poisson equation)
  • Solve time-dependent PDEs (such as the heat equation)
  • Solve non-linear PDEs
  • Solve systems of time-dependent non-linear PDEs

Important topics include: how to set boundary conditions of various types (Dirichlet, Neumann, Robin), how to create meshes, how to define variable coefficients, how to interact with linear and non-linear solvers, and how to post-process and visualize solutions

K.4 Solving the Poisson equation

Authors: Hans Petter Langtangen, Anders Logg, Jørgen S. Dokken

The goal of this section is to solve one of the most basic PDEs, the Poisson equation, with a few lines of code in FEniCSx. We start by introducing some fundamental FEniCSx objects, such as functionspace,Function, TrialFunction and TestFunction, and learn how to write a basic PDE solver. This will include:

  • How to formulate a mathematical variational problem
  • How to apply boundary conditions
  • How to solve the discrete linear system
  • How to visualize the solution

The Poisson equation is the following boundary-value problem:

\[\begin{aligned} -\nabla^2 u(\mathbf{x}) &= f(\mathbf{x})&&\mathbf{x} \in \Omega\\ u(\mathbf{x}) &= u_D(\mathbf{x})&& \mathbf{x} \in \partial\Omega \end{aligned}\]

Here, \(u=u(\mathbf{x})\) is the unknown function, \(f=f(\mathbf{x})\) is a prescribed function, \(\nabla^2\) (often written as \(\Delta\)) is the Laplace operator, \(\Omega\) is the spatial domain, and \(\partial\Omega\) is its boundary. The Poisson problem — consisting of the PDE \(-\nabla^2 u = f\) together with the boundary condition \(u=u_D\) on \(\partial\Omega\) — is a boundary value problem that must be precisely defined before we can solve it numerically with FEniCSx

  • In the two-dimensional space with coordinates \(x\) and \(y\), we can expand the Poisson equation as

\[-\frac{\partial^2 u}{\partial x^2} - \frac{\partial^2 u}{\partial y^2} = f(x,y)\]

The unknown \(u\) is now a function of two variables, \(u=u(x,y)\), defined over the two-dimensional domain \(\Omega\)

  • The Poisson equation arises in numerous physical contexts, including heat conduction, electrostatics, diffusion of substances, twisting of elastic rods, inviscid fluid flow, and water waves. Moreover, the equation appears in numerical splitting strategies for more complicated systems of PDEs, in particular the Navier–Stokes equations

Solving a boundary value problem in FEniCSx consists of the following steps:

  1. Identify the computational domain \(\Omega\), the PDE, and its corresponding boundary conditions and source terms \(f\)
  2. Reformulate the PDE as a finite element variational problem
  3. Write a Python program defining the computational domain, the boundary conditions, the variational problem, and the source terms, using FEniCSx
  4. Run the Python program to solve the boundary-value problem. Optionally, you can extend the program to derive quantities such as fluxes and averages, and visualize the results

As we have already covered step 1, we shall now cover steps 2-4

K.4.1 Finite element variational formulation

FEniCSx is based on the finite element method, which is a general and efficient mathematical technique for the numerical solution of PDEs. The starting point for finite element methods is a PDE expressed in variational form

The basic recipe for turning a PDE into a variational problem is:

  • Multiply the PDE by a function \(v\)
  • Integrate the resulting equation over the domain \(\Omega\)
  • Perform integration by parts of those terms with second order derivatives

The function \(v\) that multiplies the PDE is called a test function, while the unknown function \(u\) to be approximated is referred to as a trial function. The terms trial function and test function are also used in FEniCSx. Both test and trial functions belong to certain specific function spaces that define their properties

  • In the present case, we multiply the Poisson equation by a test function \(v\) and integrate over \(\Omega\):

    \[\int_\Omega (-\nabla^2 u) v~\mathrm{d} x = \int_\Omega f v~\mathrm{d} x\]

    Here \(\mathrm{d} x\) denotes the differential element for integration over the domain \(\Omega\). We will later let \(\mathrm{d} s\) denote the differential element for integration over \(\partial\Omega\), the boundary of \(\Omega\)

  • A rule of thumb when deriving variational formulations is that one tries to keep the order of derivatives of \(u\) and \(v\) as small as possible. Here, we have a second-order differential of \(u\), which can be transformed to a first derivative by employing the technique of integration by parts. The formula reads

    \[-\int_\Omega (\nabla^2 u)v~\mathrm{d}x = \int_\Omega\nabla u\cdot\nabla v~\mathrm{d}x - \underbrace{\int_\Omega \nabla\cdot (v\nabla u) ~\mathrm{d}x}_{\displaystyle \scriptsize\int_{\partial\Omega}\frac{\partial u}{\partial n}v~\mathrm{d}s}\]

    where \(\frac{\partial u}{\partial n}=\nabla u \cdot \mathbf{n}\) is the derivative of \(u\) in the outward normal direction \(\mathbf{n}\) on the boundary

  • Another feature of variational formulations is that the test function \(v\) must vanish on the parts of the boundary where the solution \(u\) is prescribed. In the present problem, this means that \(v = 0\) on the entire boundary \(\partial\Omega\). Consequently, the second term in the integration by parts formula vanishes, and we obtain

    \[\int_\Omega \nabla u \cdot \nabla v~\mathrm{d} x = \int_\Omega f v~\mathrm{d} x\]

  • If we require that this equation holds for all test functions \(v\) in some suitable space \(\hat{V}\), the so-called test space, we obtain a well-defined mathematical problem that uniquely determines the solution \(u\), which lies in some function space \(V\). Note that \(V\) does not necessarily coincide with \(\hat{V}\). We call the space \(V\) the trial space. The equation above is referred to as the weak form(or variational form) of the original boundary-value problem. We can now state our variational problem more precisely: \(~\) Find \(u\in V\) such that

    \[\int_\Omega \nabla u \cdot \nabla v~\mathrm{d} x = \int_\Omega f v~\mathrm{d} x\qquad \forall v \in \hat{V}\]

  • For the present problem, the trial and test spaces, \(V\) and \(\hat{V}\), are defined as follows

    \[\color{red}{\begin{aligned} V&=\{v\in H^1(\Omega) \,\vert\, v=u_D \;\text{on } \partial \Omega \}\\ \hat{V}&=\{v\in H^1(\Omega) \,\vert\, v=0 \;\text{on } \partial \Omega \} \end{aligned}}\]

    In short, \(H^1(\Omega)\) is the Sobolev space consisting of functions \(v\) for which both \(v^2\) and \(\lvert \nabla v \rvert^2\) have finite integrals over \(\Omega\). The solution of the underlying PDE must belong to a function space in which derivatives are continuous. However, the Sobolev space \(H^1(\Omega)\) also admits functions with discontinuous derivatives

    This weaker continuity requirement in the weak formulation (arising from the integration by parts) is crucial for constructing finite element function spaces. In particular, it permits the use of piecewise polynomial function spaces. Such spaces are built by stitching together polynomial functions over simple domains, such as intervals, triangles, quadrilaterals, tetrahedra, and hexahedra

  • The variational problem is a continuous problem: it defines the solution \(u\) in the infinite-dimensional function space \(V\). The finite element method for the Poisson equation approximates this solution by replacing the infinite-dimensional function spaces \(V\) and \(\hat{V}\), with discrete (finite-dimensional) spaces \(V_h\subset V\) and \(\hat{V}_h \subset \hat{V}\). The resulting discrete variational problem is then stated as: \(~\) Find \(u_h\in V_h\) such that

    \[\color{red}{ \begin{aligned} \int_\Omega \nabla u_h \cdot \nabla v~\mathrm{d} x &= \int_\Omega fv~\mathrm{d} x && \forall v \in \hat{V}_h \end{aligned}} \]

  • This variational problem, together with appropriate definitions of \(V_h\) and \(\hat{V}_h,\) uniquely determines our approximate numerical solution to the Poisson equation. Note that the boundary condition is incorporated into the trial and test spaces. While this may appear complicated at first, it ensures that the finite element variational problem has the same form as the continuous variational problem

K.4.2 Abstract finite element variational formulation

We will introduce the following notation for variational problems: \(\,\) Find \(u\in V\) such that

\[\begin{aligned} a(u,v)&=L(v)&& \forall v \in \hat{V} \end{aligned}\]

For the Poisson equation, we have:

\[\begin{aligned} a(u,v) &= \int_{\Omega} \nabla u \cdot \nabla v~\mathrm{d} x\\ L(v) &= \int_{\Omega} fv~\mathrm{d} x \end{aligned}\]

In the literature \(a(u,v)\) is known as the bilinear form and \(L(v)\) as a linear form. For every linear problem, we will identify all terms with the unknown \(u\) and collect them in \(a(u,v)\), and collect all terms with only known functions in \(L(v)\).

To solve a linear PDE in FEniCSx, such as the Poisson equation, a user thus needs to perform two steps:

  1. Choose the finite element spaces \(V\) and \(\hat{V}\) by specifying the domain (the mesh) and the type of function space (polynomial degree and type)
  2. Express the PDE as a (discrete) variational problem: \(\,\) Find \(u\in V\) such that \(a(u,v)=L(v)\) for all \(v \in \hat{V}\)

K.4.3 Implementation

In this section, you will learn:

  • How to use the built-in meshes in DOLFINx
  • How to create a spatially varying Dirichlet boundary conditions on the whole domain boundary
  • How to define a weak formulation of your PDE
  • How to solve the resulting system of linear equations
  • How to visualize the solution using a variety of tools
  • How to compute the \(L^2(\Omega)\) error and the error at mesh vertices

Up to this point, we’ve looked at the Poisson problem in very general terms: the domain \(\Omega\), the boundary condition \(u_D\), and the right-hand side \(f\) were all left unspecified. To actually solve something, we now need to pick concrete choices for \(\Omega\), \(u_D\), and \(f\)

A good strategy is to set up the problem in a way that we already know the exact solution. That way, we can easily check whether our numerical solution is correct. Polynomials of low degree are usually the best choice here, because continuous Galerkin finite element spaces of degree \(r\) can reproduce any polynomial of degree \(r\) exactly

  • To test our solver, we’ll construct a problem where we already know the exact solution. This approach is known as the method of manufactured solutions. The idea is simple:

    1. Start by picking a function \(u_e(x,y)\) that looks nice and simple
    2. Plug \(u_e\) into the PDE to figure out what the right-hand side \(f(x,y)\) should be
    3. Use \(u_e\) as the boundary condition \(u_D\)
    4. Finally, solve the problem numerically and compare the computed solution with \(u_e\)

Step 1: Choosing the exact solution

Let’s take a quadratic function in 2D:

\[ u_e(x,y) = 1 + x^2 + 2y^2 \]

Step 2: Computing the source term

If we insert \(u_e\) into the Poisson equation, we obtain

\[f(x,y) = -6, \;\; u_D(x,y) = u_e(x,y) = 1 + x^2 + 2y^2\]

Notice that this holds regardless of the domain shape, as long as we prescribe \(u_e\) on the boundary

Step 3: Choosing the domain

For simplicity, let’s use the unit square:

\[\Omega = [0,1] \times [0,1]\]

Step 4: Summary

This small example illustrates a very powerful strategy:

  • Pick an exact solution
  • Plug it into the PDE to generate the corresponding source term
  • Solve the PDE with these inputs
  • Verify that the numerical solution reproduces the exact solution

This workflow is at the heart of the method of manufactured solutions, and it provides a simple but rigorous way to validate our solver

Generating simple meshes

The next step is to define the discrete domain, called the mesh. We do this using one of FEniCSx’s built-in mesh generators

Here, we create a unit square mesh spanning \([0,1]\times[0,1]\). The cells of the mesh can be either triangles or quadrilaterals:

import numpy as np

from mpi4py import MPI
from dolfinx import mesh

N = 8
domain = mesh.create_unit_square(
  MPI.COMM_WORLD, 
  nx=N, 
  ny=N, 
  cell_type=mesh.CellType.quadrilateral
)

Notice that we need to provide an MPI communicator. This determines how the program behaves in parallel:

  • If we pass MPI.COMM_WORLD, a single mesh is created and distributed across the number of processors we specify. For example, to run the program on two processors, we can use:
$ mpirun -n 2 python tutorial_poisson.py
  • If instead we use MPI.COMM_SELF, each processor will create its own independent copy of the mesh. This can be useful when running many small problems in parallel, for example when sweeping over different parameters

Defining the finite element function space

Once the mesh is created, the next step is to define the finite element function space \(V\). DOLFINx supports a wide variety of finite element spaces of arbitrary order. For a full overview, see the list of Supported elements in DOLFINx

When creating a function space, we need to specify:

  1. The mesh on which the space is defined
  2. The element family (e.g., Lagrange, Raviart–Thomas, etc.)
  3. The polynomial degree of the element

In DOLFINx, this can be done by passing a tuple of the form ("family", degree), as shown below:

from dolfinx import fem

V = fem.functionspace(domain, ("Lagrange", 1))

See Degree 1 Lagrange on a quadrilateral

The next step is to create a function that stores the Dirichlet boundary condition. We then use interpolation to fill this function with the prescribed values

uD = fem.Function(V)
uD.interpolate(lambda x: 1 +x[0]**2 +2 *x[1]**2)

With the boundary data defined (which, in this case, coincides with the exact solution of our finite element problem), we now need to enforce it along the boundary of the mesh

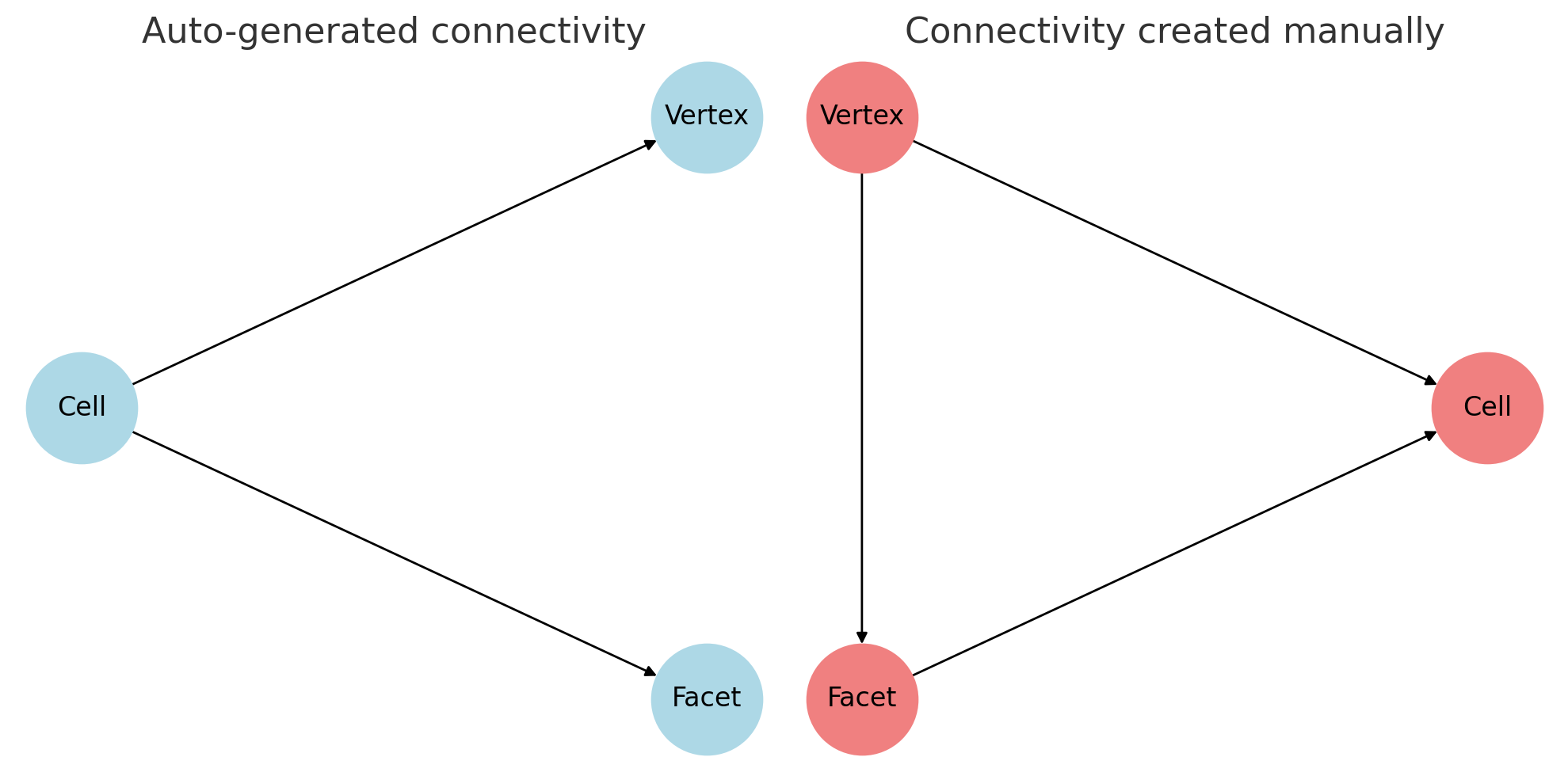
The first step is to identify which parts of the mesh correspond to the outer boundary. In DOLFINx, the boundary is represented by facets (that is, the line segments making up the outer edges in 2D or surfaces in 3D).

We can extract the indices of all exterior facets using:

tdim = domain.topology.dim
fdim = tdim -1

domain.topology.create_connectivity(fdim, tdim)
boundary_facets = mesh.exterior_facet_indices(domain.topology)

This gives us the set of facets lying on the boundary of our discrete domain. Once we know where the boundary is, we can proceed to apply the Dirichlet boundary conditions to all degrees of freedom (DoFs) located on these facets

For our current problem, we are using the “Lagrange” degree-1 function space. In this case, the degrees of freedom (DoFs) are located at the vertices of each cell, so every boundary facet contains exactly two DoFs

To identify the local indices of these boundary DoFs, we use dolfinx.fem.locate_dofs_topological. This function takes three arguments:

  1. the function space
  2. the dimension of the mesh entities we want to target, and
  3. the list of entities (in our case, the boundary facets)

Once we have the boundary DoFs, we can create the Dirichlet boundary condition as follows:

boundary_dofs = fem.locate_dofs_topological(V, fdim, boundary_facets)
bc = fem.dirichletbc(uD, boundary_dofs)

Defining the trial and test function

In mathematics, we usually distinguish between the trial space \(V\) and the test space \(\hat{V}\). For the present problem, the only difference between the two would be the treatment of boundary conditions

In FEniCSx, however, boundary conditions are not built directly into the function space. This means we can simply use the same space for both the trial and test functions

To express the variational formulation, we make use of the Unified Form Language (UFL)

import ufl

u = ufl.TrialFunction(V)
v = ufl.TestFunction(V)

Defining the source term

Since the source term is constant throughout the domain, we can represent it using dolfinx.fem.Constant:

from dolfinx import default_scalar_type

f = fem.Constant(domain, default_scalar_type(-6))

While we could simply define the source term as f = -6, this has a limitation: if we later want to change its value, we would need to redefine the entire variational problem. By using dolfinx.fem.Constant, we can easily update the value during the simulation, for example with f.value = 5

Another advantage is performance: declaring f as a constant allows the compiler to optimize the variational formulation, leading to faster assembly of the resulting linear system

Defining the variational problem

Now that we have defined all the components of our variational problem, we can write down the weak formulation:

a = ufl.dot(ufl.grad(u), ufl.grad(v)) *ufl.dx
L = f *v *ufl.dx

Notice how closely the Python syntax mirrors the mathematical expressions:

\[a(u,v) = \int_{\Omega} \nabla u \cdot \nabla v \,\mathrm{d}x, \;\; L(v) = \int_{\Omega} f v \,\mathrm{d}x\]

Here, ufl.dx represents integration over the domain \(\Omega\), i.e. over all cells of the mesh. This illustrates one of the major strengths of FEniCSx: \(\,\) variational formulations can be written in Python in a way that almost directly matches their mathematical form, making it both natural and convenient to specify and solve complex PDE problems

Expressing inner products

The inner product

\[\int_\Omega \nabla u \cdot \nabla v \,\mathrm{d}x\]

can be expressed in different ways in UFL. In our example, we wrote it as: ufl.dot(ufl.grad(u), ufl.grad(v)) *ufl.dx. In UFL, the dot operator performs a contraction: it sums over the last index of the first argument and the first index of the second argument. Since both \(\nabla u\) and \(\nabla v\) are rank-1 tensors (vectors), this reduces to a simple dot product.

For higher-rank tensors, such as matrices (rank-2 tensors), the appropriate operator is ufl.inner, which computes the full Frobenius inner product. For vectors, however, ufl.dot and ufl.inner are equivalent

Forming and solving the linear system

Having defined the finite element variational problem and boundary conditions, we can now create a dolfinx.fem.petsc.LinearProblem. This class provides a convenient interface for solving

Find \(u_h\in V\) such that \(a(u_h, v)=L(v), \;\; \forall v \in \hat{V}\)

In this example, we will use PETSc as the linear algebra backend, together with a direct solver (LU factorization)

For more details on Krylov subspace(KSP) solvers and preconditioners, see the PETSc-documentation. Note that PETSc is not a required dependency of DOLFINx, so we explicitly import the DOLFINx wrapper to interface with PETSc. Finally, to ensure that the solver options passed to the LinearProblem apply only to this specific KSP solver, we assign a unique option prefix

from dolfinx.fem.petsc import LinearProblem

problem = LinearProblem(
    a, L, bcs=[bc],
    petsc_options={
        # Direct solver using LU factorization
        "ksp_type": "preonly",
        "pc_type": "lu"
    }
)

# Solve the system
uh = problem.solve()

# Optionally, view solver information
#ksp = problem.solver
#ksp.view()

The ksp_type option in PETSc KSP solver specifies which algorithm to use for solving the linear system, while pc_type specifies the type of preconditioner. For most FEM problems, Symmetric Positive Definite(SPD) systems typically use cg with ilu or amg, and if a direct LU solver is desired, one can use ksp_type="preonly" with pc_type="lu"

Using problem.solve(), we solve the linear system of equations and return a dolfinx.fem.Function containing the solution

Computing the error

Finally, we want to compute the error to check the accuracy of the solution. We do this by comparing the finite element solution uh with the exact solution. We do this by interpolating the exact solution into the the \(P_2\)-function space

V2 = fem.functionspace(domain, ("Lagrange", 2))
uex = fem.Function(V2)
uex.interpolate(lambda x: 1 +x[0]**2 +2 *x[1]**2)

We compute the error in two different ways. First, we compute the \(L^2\) norm of the error, defined by

\[E=\sqrt{\int_\Omega (u_D-u_h)^2 \,\mathrm{d} x}\]

We use UFL to express the \(L^2\) error, and use dolfinx.fem.assemble_scalar to compute the scalar value. In DOLFINx, assemble_scalar only assembles over the cells on the local process. This means that if we use 2 processes to solve our problem, we need to gather the solution to one. We can do this with the MPI.allreduce function

L2_error = fem.form(ufl.inner(uh -uex, uh -uex) *ufl.dx)
error_local = fem.assemble_scalar(L2_error)
error_L2 = np.sqrt(domain.comm.allreduce(error_local, op=MPI.SUM))

Secondly, we compute the maximum error at any degree of freedom (dof). The finite element solution uh can be expressed as a linear combination of the basis functions \(\phi_j\) spanning the space \(V\):

\[u = \sum_{j=1}^N U_j \phi_j\]

When we call problem.solve(), we obtain all coefficients \(U_1\), \(\dots\), \(U_N\). These coefficients are the degrees of freedom (dofs). We can access the dofs by retrieving the underlying vector from uh

However, note that a second-order function space contains more dofs than a first-order space, so the corresponding arrays cannot be compared directly. Fortunately, since we have already interpolated the exact solution into the first-order space when defining the boundary condition, we can compare the maximum values at the dofs of the approximation space

error_max = np.max(np.abs(uD.x.array -uh.x.array))

# Only print the error on one process
if domain.comm.rank == 0:
    print(f"Error_L2 : {error_L2:.2e}")
    print(f"Error_max : {error_max:.2e}")
Error_L2 : 8.24e-03
Error_max : 5.33e-15

Plotting the mesh using pyvista

First, prepare a folder to store the output figures as follows:

from pathlib import Path

results_folder = Path("fenicsx/fundamentals")
results_folder.mkdir(exist_ok=True, parents=True)

We will visualize the mesh using pyvista, a Python interface to the VTK toolkit. To begin, We convert the mesh into a format compatible with pyvista using the function dolfinx.plot.vtk_mesh. The first step is to create an unstructured grid that pyvista can work with

You can check the current plotting backend with:

import pyvista
from dolfinx import plot

topology, cell_types, geometry = plot.vtk_mesh(domain, tdim)
grid = pyvista.UnstructuredGrid(topology, cell_types, geometry)

PyVista supports several backends, each with its own advantages and limitations. For more information and installation instructions, see the pyvista documentation

We can now use the pyvista.Plotter to visualize the mesh. We will display it both as a 2D and as a 3D warped representation. Provided that a proper X server connection is available, the default setting pyvista.OFF_SCREEN=False can be used to render the plots directly within the notebook

plotter = pyvista.Plotter(off_screen=True)
plotter.add_mesh(grid, show_edges=True)
plotter.add_axes()
plotter.view_xy()

# if not pyvista.OFF_SCREEN:
#   plotter.show()

# HTML 저장
plotter.export_html("fenicsx/fundamentals/unit_square_mesh.html")

Plotting a function using pyvista

We want to plot the solution uh. Since the function space used to define uh is disconnected from the one used to define the mesh, we first create a mesh based on the DoF coordinates of the function space V. We then use dolfinx.plot.vtk_mesh, passing the function space as input, to generate a mesh whose geometry is based on these DoF coordinates

u_topology, u_cell_types, u_geometry = plot.vtk_mesh(V)

Next, we create the pyvista.UnstructuredGrid and add the DoF-values to the mesh

u_grid = pyvista.UnstructuredGrid(u_topology, u_cell_types, u_geometry)
u_grid.point_data["u"] = uh.x.array.real
u_grid.set_active_scalars("u")

u_plotter = pyvista.Plotter(off_screen=True)
u_plotter.add_mesh(
    u_grid, 
    show_edges=True,
    scalar_bar_args={
        "title": "u",
        "fmt": "%.1f",
        "color": "black",
        "label_font_size": 12,
        # "vertical": True,
        "n_labels": 7,
    },
)
u_plotter.add_axes()
u_plotter.view_xy()

# if not pyvista.OFF_SCREEN:
#     u_plotter.show()

# HTML 저장
u_plotter.export_html("fenicsx/fundamentals/poisson_solution_2D.html")

External post-processing

For post-processing outside Python, it is recommended to save the solution to a file using either dolfinx.io.VTXWriter or dolfinx.io.XDMFFile, and then visualize it in ParaView. This approach is especially useful for 3D visualization

from dolfinx import io

filename = results_folder/"poisson"

with io.VTXWriter(domain.comm, filename.with_suffix(".bp"), [uh]) as vtx:
    vtx.write(0.0)
    
with io.XDMFFile(domain.comm, filename.with_suffix(".xdmf"), "w") as xdmf:
    xdmf.write_mesh(domain)
    xdmf.write_function(uh)

K.5 Weak imposition of Dirichlet conditions for the Poisson problem

Author: Jørgen S. Dokken

This section shows how to solve the previous Poisson problem using Nitsche’s method. Weak imposition works by adding terms to the variational formulation to enforce the boundary condition, instead of altering the matrix system via strong imposition (lifting)

First, we import the necessary modules and set up the mesh and function space for the solution

import numpy as np
from mpi4py import MPI

from dolfinx import fem, mesh, plot, default_scalar_type
from dolfinx.fem.petsc import LinearProblem

from ufl import (
  Circumradius, 
  FacetNormal, 
  SpatialCoordinate, 
  TrialFunction, 
  TestFunction,
  dx, 
  ds, 
  div, 
  grad, 
  inner,
)

N = 8
domain = mesh.create_unit_square(MPI.COMM_WORLD, N, N)
V = fem.functionspace(domain, ("Lagrange", 1))

Next, we create a function for the exact solution (also used in the Dirichlet boundary condition) and the corresponding source function for the right-hand side. The exact solution is defined using ufl.SpatialCoordinate, then interpolated into uD and used to generate the source function f

x = SpatialCoordinate(domain)
u_ex = 1 +x[0]**2 +2 *x[1]**2

uD = fem.Function(V)
uD.interpolate(fem.Expression(u_ex, V.element.interpolation_points()))
f = -div(grad(u_ex))

Unlike the first tutorial, we now need to revisit the variational form. We begin by integrating the problem by parts to obtain

\[\begin{aligned} \int_{\Omega} \nabla u \cdot \nabla v~\mathrm{d}x - \int_{\partial\Omega}\nabla u \cdot \mathbf{n}\, v~\mathrm{d}s = \int_{\Omega} f v~\mathrm{d}x \end{aligned}\]

As we are not enforcing the boundary condition strongly, the trace of the test function is not set to zero on the boundary. We instead add the following two terms to the variational formulation:

\[\begin{aligned} -\int_{\partial\Omega} \nabla v \cdot \mathbf{n}\, (u-u_D)~\mathrm{d}s + \frac{\alpha}{h} \int_{\partial\Omega} (u-u_D)v~\mathrm{d}s \end{aligned}\]

The first term enforces symmetry in the bilinear form, and the second term ensures coercivity. \(u_D\) denotes the known Dirichlet condition, and \(h\) is the diameter of the circumscribed sphere of the mesh element. The bilinear and linear forms, \(a\) and \(L\), are then defined as

\[\begin{aligned} a(u, v) &= \int_{\Omega} \nabla u \cdot \nabla v ~\mathrm{d}x + \int_{\partial\Omega} -(\mathbf{n}\, \cdot\nabla u) v - (\mathbf{n}\, \cdot \nabla v) u + \frac{\alpha}{h} uv ~\mathrm{d}s \\ L(v) &= \int_{\Omega} fv ~\mathrm{d}x + \int_{\partial\Omega} -(\mathbf{n}\, \cdot \nabla v) u_D + \frac{\alpha}{h} u_D v ~\mathrm{d}s \end{aligned}\]

u = TrialFunction(V)
v = TestFunction(V)

n = FacetNormal(domain)
h = 2 *Circumradius(domain)
alpha = fem.Constant(domain, default_scalar_type(10))

a = inner(grad(u), grad(v)) *dx -inner(n, grad(u)) *v *ds
a += -inner(n, grad(v)) *u *ds +alpha /h *inner(u, v) *ds
L = inner(f, v) *dx 
L += -inner(n, grad(v)) *uD *ds +alpha /h *inner(uD, v) *ds

With the variational form in place, we can solve the linear problem

problem = LinearProblem(a, L)
uh = problem.solve()

We compute the error by comparing the numerical solution with the analytical solution

error_form = fem.form(inner(uh -uD, uh -uD) *dx)
error_local = fem.assemble_scalar(error_form)
error_L2 = np.sqrt(domain.comm.allreduce(error_local, op=MPI.SUM))
if domain.comm.rank == 0:
    print(f"Error_L2: {error_L2:.2e}")
Error_L2: 1.59e-03

The \(L^2\)-error has the same order of magnitude as in the first tutorial, and we also compute the maximum error over all degrees of freedom

error_max = domain.comm.allreduce(
  np.max(np.abs(uD.x.array -uh.x.array)), 
  op=MPI.MAX)
if domain.comm.rank == 0:
    print(f"Error_max : {error_max:.2e}")
Error_max : 5.41e-03

We observe that, due to the weak imposition of the boundary condition, the equation is not satisfied to machine precision at the mesh vertices. The solution is subsequently visualized using pyvista

import pyvista

u_grid = pyvista.UnstructuredGrid(*plot.vtk_mesh(V))
u_grid.point_data["u"] = uh.x.array.real
u_grid.set_active_scalars("u")

u_plotter = pyvista.Plotter(off_screen=True)
u_plotter.add_mesh(
  u_grid, 
  show_edges=True, 
  scalar_bar_args={
        "title": "u",
        "fmt": "%.1f",
        "color": "black",
        "label_font_size": 12,
        # "vertical": True,
        "n_labels": 7,
  },  
  show_scalar_bar=True
)

u_plotter.add_axes()
u_plotter.view_xy()

# if not pyvista.OFF_SCREEN:
#     u_plotter.show()

# HTML 저장
u_plotter.export_html(
  "fenicsx/fundamentals/poisson_nitsche_solution_2D.html"
)

K.6 Deflection of a membrane

Authors: Hans Petter Langtangen, Anders Logg, Jørgen S. Dokken

In the first FEniCSx example, we addressed a simple, easily verifiable problem. In this section, we consider a more physically relevant case that produces solutions with richer structure. In particular, we compute the deflection \(D(x,y)\) of a two-dimensional circular membrane of radius \(R\), under a load distribution \(p(x,y)\). The governing PDE is:

\[ \begin{aligned} -T \nabla^2D&=p \quad\text{in }\; \Omega=\{(x,y)\,\vert\, x^2+y^2\leq R^2 \} \end{aligned} \]

Here, \(T\) denotes the constant membrane tension, and \(p\) represents the external pressure load. The boundary of the membrane is fixed, implying the boundary condition \(D=0\). We model a localized load using a Gaussian function:

\[ \begin{aligned} p(x,y)&=\frac{A}{2\pi\sigma}\exp\left(-\frac{1}{2}\left[\left(\frac{x-x_0}{\sigma}\right)^2 +\left(\frac{y-y_0}{\sigma}\right)^2\right] \right) \end{aligned} \]

where \(A\) is the load amplitude, \((x_0, y_0)\) is the location of the load maximum, and \(\sigma\) characterizes the width of \(p\). We place the load center at \((x_0, y_0) = (0, R_0)\), with \(0 < R_0 < R\). The resulting expression becomes

\[ \begin{aligned} p(x,y)&=\frac{A}{2\pi\sigma}\exp\left(-\frac{1}{2}\left[\left(\frac{x}{\sigma}\right)^2 +\left(\frac{y-R_0}{\sigma}\right)^2\right]\right) \end{aligned} \]

K.6.1 Scaling the equation

This problem involves several physical parameters, and it is useful to simplify the formulation by introducing dimensionless variables. We define the scaled coordinates \(\bar{x} = \tfrac{x}{R}\), \(\bar{y} = \tfrac{y}{R}\), and the dimensionless deflection \(w = \tfrac{D}{D_e}\), where \(D_e\) is a characteristic deflection. Introducing \(\bar{R}_0 = \tfrac{R_0}{R}\), we obtain

\[ \begin{aligned} -\left(\frac{\partial^2 w}{\partial \bar{x}^2} +\frac{\partial^2 w}{\partial \bar{y}^2} \right) &=\frac{R^2A}{2\pi\sigma TD_e} \exp\left(-\frac{R^2}{2\sigma^2}\left[\bar{x}^2+(\bar{y}-\bar{R}_0)^2\right]\right)\\ &=\alpha \exp\left(-\beta^2 \left[\bar{x}^2+(\bar{y}-\bar{R}_0)^2\right]\right) \end{aligned} \]

valid for \(\bar{x}^2+\bar{y}^2<1\), where \(\alpha = \frac{R^2A}{2\pi\sigma TD_e}\) and \(\beta=\frac{R}{\sqrt{2}\sigma}\)

With an appropriate scaling, both \(w\) and its derivatives are of order unity. Consequently, the left-hand side of the scaled PDE is also of order unity, while the right-hand side is governed by the parameter \(\alpha\). This motivates choosing \(\alpha\) to be of order one; in this case, we set \(\alpha = 4\). (Alternatively, one can derive the analytical solution in scaled coordinates and verify that the maximum deflection equals \(D_e\) when \(\alpha = 4\), which provides the definition of \(D_e\))

With \(D_e = \tfrac{R^2 A}{8 \pi \sigma T}\) and omitting the overbars, the scaled problem becomes

\[-\nabla^2 w = 4 \exp\left(-\beta^2 \left[x^2 + (y-R_0)^2\right]\right)\]

to be solved over the unit disk, with \(w=0\) on the boundary

In the nondimensional formulation, the problem depends only on two parameters: the dimensionless width of the pressure distribution \(\beta\) and the location of the pressure maximum \(R_0 \in [0,1]\). In the limit \(\beta \to 0\), the solution converges to the special case \(w = 1 - x^2 - y^2\)

Given a computed scaled solution \(w\), the corresponding physical deflection is recovered as

\[ \begin{aligned} D=\frac{AR^2}{8\pi\sigma T}w \end{aligned} \]

K.6.2 Implementation

Author: Jørgen S. Dokken

In this section, we will solve the membrane deflection problem. By the end of this section, you should be able to:

  • Construct a simple mesh using the GMSH Python API and import it into DOLFINx
  • Specify constant boundary conditions via a geometrical identifier
  • Employ ufl.SpatialCoordinate to define a spatially varying function
  • Interpolate a ufl.Expression into a suitable function space
  • Evaluate a dolfinx.Function at arbitrary points

Creating the mesh

To construct the computational geometry, we use the Python API of GMSH. We begin by importing the gmsh module and initializing it

# $ conda install -c conda-forge python-gmsh
import gmsh

if not gmsh.isInitialized():
    gmsh.initialize()

Next, we define the membrane geometry and begin the setup using the GMSH CAD kernel, which automatically generates the required data structures in the background. When calling addDisk, the first three arguments specify the \(x,\) \(y,\) and \(z\) coordinates of the circle’s center, while the final two define the radii in the \(x\)- and \(y\)-directions

# gmsh.model.occ.addDisk(xc, yc, zc, rx, ry)
#   xc, yc, zc : center coordinates
#   rx, ry     : radii in x- and y-directions
membrane = gmsh.model.occ.addDisk(0.0, 0.0, 0.0, 1, 1)

# Synchronize the CAD kernel with the gmsh model
gmsh.model.occ.synchronize()

Next, we define the membrane as a physical surface so that GMSH will recognize it during mesh generation. Because a surface is a two-dimensional entity, we pass 2 as the first argument, the membrane’s entity tag as the second, and the physical tag as the last. In a later example, we will explain in more detail when and why this physical tag becomes important

gdim = 2
physical_tag = 1

# Remove any existing physical groups with the same (dim, tag)
for dim, tag in gmsh.model.getPhysicalGroups():
    if dim == gdim and tag == physical_tag:
        gmsh.model.removePhysicalGroups([(dim, tag)])

# Now safely add the new physical group
pg = gmsh.model.addPhysicalGroup(gdim, [membrane], physical_tag)
gmsh.model.setPhysicalName(gdim, pg, "Circular Membrane")

Finally, we generate the two-dimensional mesh, setting a uniform element size by adjusting the GMSH options

gmsh.option.setNumber("Mesh.CharacteristicLengthMin", 0.05)
gmsh.option.setNumber("Mesh.CharacteristicLengthMax", 0.05)
gmsh.model.mesh.generate(gdim)
Info    : Meshing 1D...
Info    : Meshing curve 1 (Ellipse)
Info    : Done meshing 1D (Wall 0.000675292s, CPU 0.000709s)
Info    : Meshing 2D...
Info    : Meshing surface 1 (Plane, Frontal-Delaunay)
Info    : Done meshing 2D (Wall 0.051716s, CPU 0.081455s)
Info    : 1552 nodes 3103 elements

Interfacing with GMSH in DOLFINx

We import the GMSH-generated mesh directly into DOLFINx using the dolfinx.io.gmshio interface. In this example, we did not specify which process created the GMSH model, so a copy of the model is created on each MPI process. However, our goal is to work with a single mesh distributed across all processes. To accomplish this, we take the model generated on rank 0 of MPI.COMM_WORLD and distribute it to all available ranks

The import also provides two sets of mesh tags: one for cells defined by physical groups and one for facets defined by physical groups. Since we did not add any physical groups of dimension gdim -1, the facet_tags object will be empty

from mpi4py import MPI
from dolfinx.io import gmshio
from dolfinx.fem.petsc import LinearProblem

domain, cell_tags, facet_tags = gmshio.model_to_mesh(
  gmsh.model, 
  MPI.COMM_WORLD, 
  rank=0, 
  gdim=gdim
)

gmsh.finalize()

We define the function space as in the previous tutorial

from dolfinx import fem, plot

V = fem.functionspace(domain, ("Lagrange", 1))
import pyvista

# Extract topology from mesh and create pyvista mesh
topology, cell_types, x = plot.vtk_mesh(V)
grid = pyvista.UnstructuredGrid(topology, cell_types, x)

plotter = pyvista.Plotter(off_screen=True)
plotter.add_mesh(grid, show_edges=True)
plotter.add_axes()
plotter.view_xy()

# if not pyvista.OFF_SCREEN:
#     plotter.show()

# HTML 저장
plotter.export_html("fenicsx/fundamentals/membrane_mesh.html")

Defining a spatially varying load

The pressure function on the right-hand side is defined with ufl.SpatialCoordinate and two constants, \(\beta\) and \(R_0\)

from dolfinx import default_scalar_type
import ufl

x = ufl.SpatialCoordinate(domain)

beta = fem.Constant(domain, default_scalar_type(12))
R0 = fem.Constant(domain, default_scalar_type(0.3))

p = 4 *ufl.exp(-beta**2 *(x[0]**2 +(x[1] -R0)**2))

Interpolation of a ufl expression

Since the load p is defined as a spatially varying function, we interpolate it into an appropriate function space for visualization. To do this, we use dolfinx.Expression, which accepts any UFL expression together with a set of points on the reference element. In practice, we provide the interpolation points of the target space. Because p exhibits rapid spatial variation, we select a high-order function space to represent it

Q = fem.functionspace(domain, ("Lagrange", 5))
expr = fem.Expression(p, Q.element.interpolation_points())

pressure = fem.Function(Q)
pressure.interpolate(expr)

We next plot the load on the domain

p_grid = pyvista.UnstructuredGrid(*plot.vtk_mesh(Q))
p_grid.point_data["p"] = pressure.x.array.real

warped_p = p_grid.warp_by_scalar("p", factor=0.5)
warped_p.set_active_scalars("p")

load_plotter = pyvista.Plotter(off_screen=True)
load_plotter.add_mesh(
  warped_p,
  show_edges=True, 
  show_scalar_bar=True,
  cmap="jet"
)
load_plotter.add_axes() 

# if not pyvista.OFF_SCREEN:
#     load_plotter.show()

# HTML 저장
load_plotter.export_html("fenicsx/fundamentals/membrane_load.html")

Create a Dirichlet boundary condition using geometrical conditions

The next step is to define the homogeneous boundary condition. Unlike in the first tutorial, we use dolfinx.fem.locate_dofs_geometrical to identify the degrees of freedom on the boundary. Since our domain is the unit circle, these degrees of freedom correspond to coordinates \((x, y)\) such that \(\sqrt{x^2 + y^2} = 1\)

import numpy as np

def on_boundary(x):
    return np.isclose(np.sqrt(x[0]**2 +x[1]**2), 1)

boundary_dofs = fem.locate_dofs_geometrical(V, on_boundary)

Since our Dirichlet condition is homogeneous (u=0 on the entire boundary), we can define it using dolfinx.fem.dirichletbc by specifying a constant value, the boundary degrees of freedom and the function space on which it should be applied

bc = fem.dirichletbc(default_scalar_type(0), boundary_dofs, V)

Defining and solving the variational problem

The variational problem is identical to our first Poisson problem, with p replacing f

u = ufl.TrialFunction(V)
v = ufl.TestFunction(V)

a = ufl.dot(ufl.grad(u), ufl.grad(v)) *ufl.dx
L = p *v *ufl.dx

problem = LinearProblem(
  a, 
  L, 
  bcs=[bc], 
  petsc_options={"ksp_type": "preonly", "pc_type": "lu"}
)
uh = problem.solve()

We plot the deflection uh over the domain \(\Omega\)

# Set deflection values and add it to plotter
grid.point_data["u"] = uh.x.array
warped = grid.warp_by_scalar("u", factor=25)

u_plotter = pyvista.Plotter(off_screen=True)
u_plotter.add_mesh(
  warped, 
  show_edges=True, 
  show_scalar_bar=True, 
  scalars="u",
  cmap='jet'
)
u_plotter.add_axes() 

# if not pyvista.OFF_SCREEN:
#     u_plotter.show()

# HTML 저장
u_plotter.export_html("fenicsx/fundamentals/membrane_u.html")

Plotting along a line in the domain

A convenient way to compare the load and deflection is by plotting them along \(x=0\), using a set of points along the \(y\)-axis to evaluate the finite element functions \(u\) and \(p\)

tol = 0.001  # Avoid hitting the outside of the domain
y = np.linspace(-1 +tol, 1 -tol, 101)

points = np.zeros((3, 101))
points[1] = y
u_values = []
p_values = []

A finite element function can be expressed as a linear combination of all its degrees of freedom:

\[u_h(x) = \sum_{i=1}^N c_i \, \phi_i(x)\]

where \(c_i\) are the coefficients of \(u_h\) and \(\phi_i\) are the basis functions. In principle, this allows us to evaluate the solution at any point in \(\Omega\)

However, since a mesh typically contains a large number of degrees of freedom (i.e., \(N\) is large), evaluating every basis function at each point would be inefficient. Instead, we first identify which mesh cell contains the point \(x\). This can be done efficiently using a bounding box tree, which enables a fast recursive search through the mesh cells

from dolfinx import geometry

bb_tree = geometry.bb_tree(domain, domain.topology.dim)

We can now determine which cells each point intersects by using dolfinx.geometry.compute_collisions_points. This function returns, for every input point, a list of cells whose bounding boxes overlap with that point. Since different points may correspond to a varying number of cells, the results are stored in a dolfinx.cpp.graph.AdjacencyList_int32. The cells associated with the \(i\)-th point can be accessed with links(i)

Because a cell’s bounding box generally extends beyond the cell itself in \(\mathbb{R}^n\), we must verify whether the point actually inside the cell. This is done with dolfinx.geometry.compute_colliding_cells, which computes the exact distance between the point and the cell (approximating higher-order cells as convex hulls). Like the previous function, it also returns an adjacency list, since a point may lie on a facet, edge, or vertex shared by multiple cells

Finally, to ensure that the code runs correctly in parallel when the mesh is distributed across multiple processors, we create a subset, points_on_proc, that includes only the points located on the current processor

cells = []
points_on_proc = []

# Find cells whose bounding-box collide with the the points
cell_candidates = geometry.compute_collisions_points(
  bb_tree, 
  points.T
)

# Choose one of the cells that contains the point
colliding_cells = geometry.compute_colliding_cells(
  domain, 
  cell_candidates, 
  points.T
)

for i, point in enumerate(points.T):
    if len(colliding_cells.links(i)) > 0:
        points_on_proc.append(point)
        cells.append(colliding_cells.links(i)[0])

We now have a list of points associated with the processor and the cell each point belongs to. This allows us to use uh.eval and pressure.eval to compute the function values at these points

points_on_proc = np.array(points_on_proc, dtype=np.float64)

u_values = uh.eval(points_on_proc, cells)
p_values = pressure.eval(points_on_proc, cells)

With the coordinates and the corresponding function values, we can now plot the results using matplotlib

import matplotlib.pyplot as plt

fig = plt.figure()

plt.plot(points_on_proc[:, 1], 50 *u_values, 
  "k", lw=2, label="Deflection ($\\times 50$)")
plt.plot(points_on_proc[:, 1], p_values, 
  "b--", lw=2, label="Load")

plt.grid(True)
plt.legend()
plt.xlabel("y")
plt.show()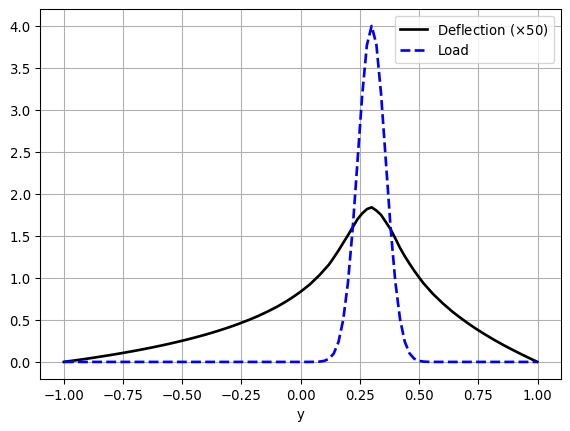

Saving functions to file

To visualize the solution in ParaView, we can save it to a file as follows:

from pathlib import Path
import dolfinx.io

results_folder = Path("fenicsx/fundamentals")
results_folder.mkdir(exist_ok=True, parents=True)

filename = results_folder/"membrane"

pressure.name = "Load"
uh.name = "Deflection"

with dolfinx.io.VTXWriter(
  MPI.COMM_WORLD, results_folder/"membrane_pressure.bp", 
  [pressure], engine="BP4") as vtx:
    vtx.write(0.0)

with dolfinx.io.VTXWriter(
  MPI.COMM_WORLD, results_folder/"membrane_deflection.bp", 
  [uh], engine="BP4") as vtx:
    vtx.write(0.0)

K.8 Subdomains and boundary conditions

K.8.1 Combining Dirichlet and Neumann conditions

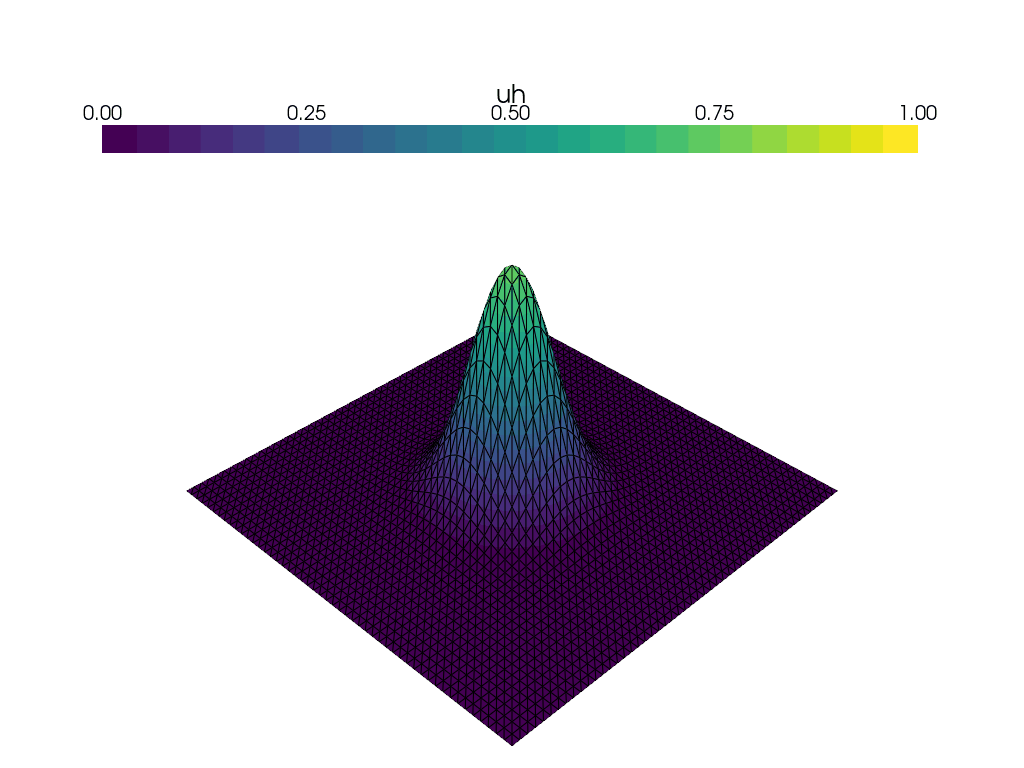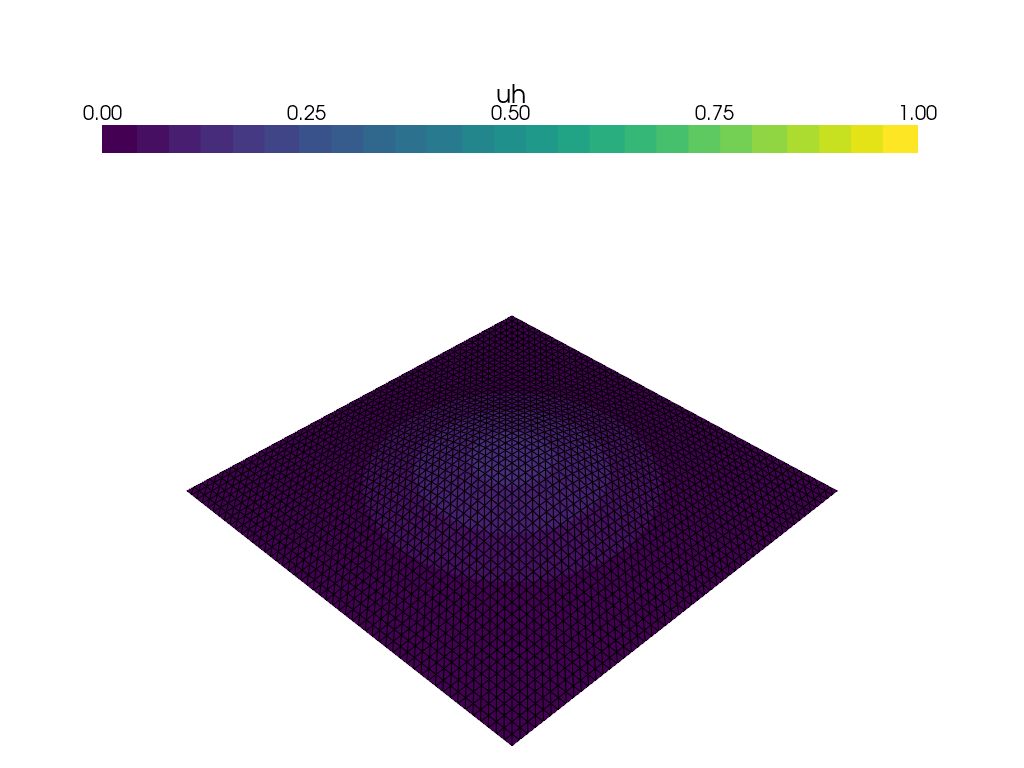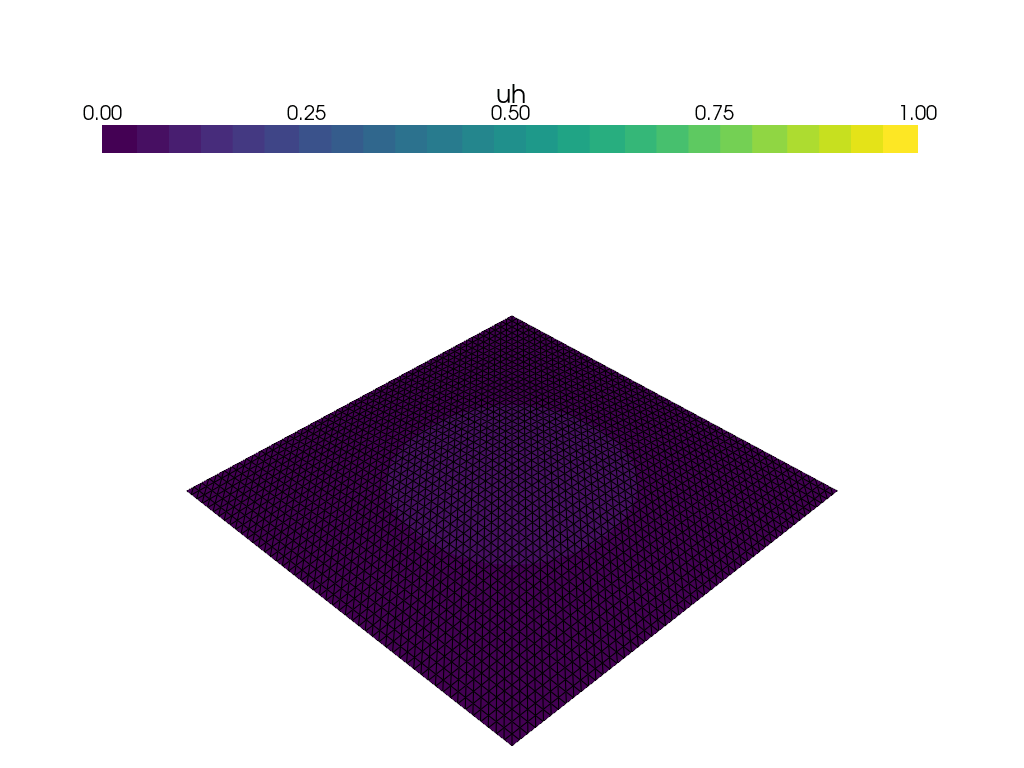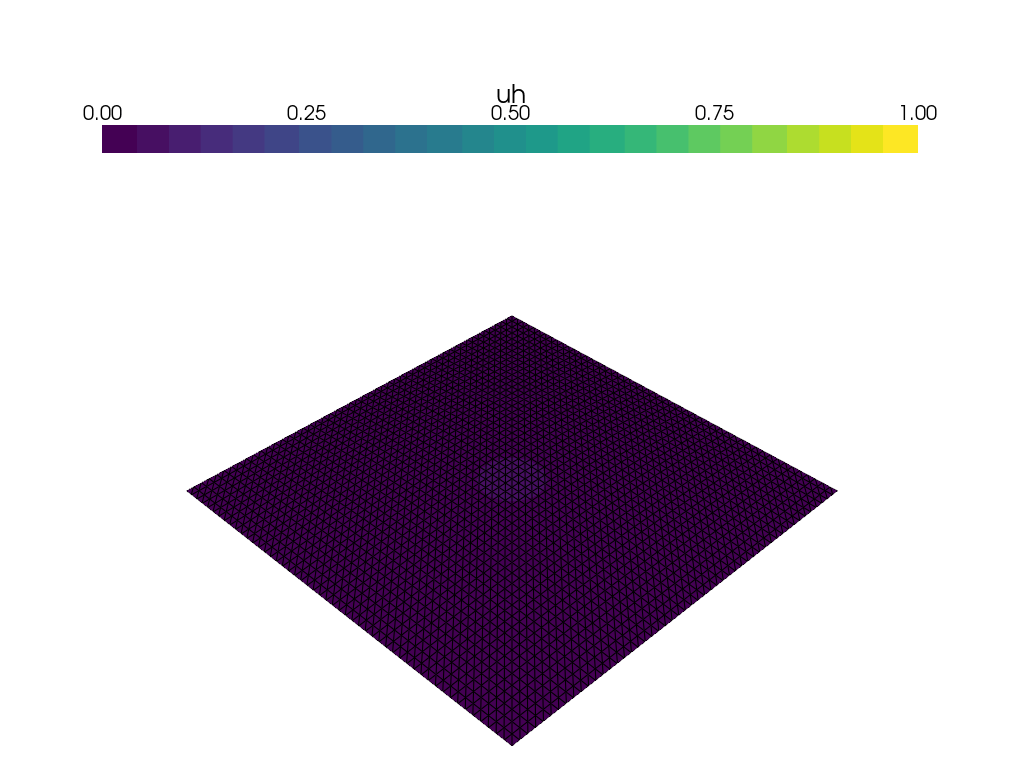
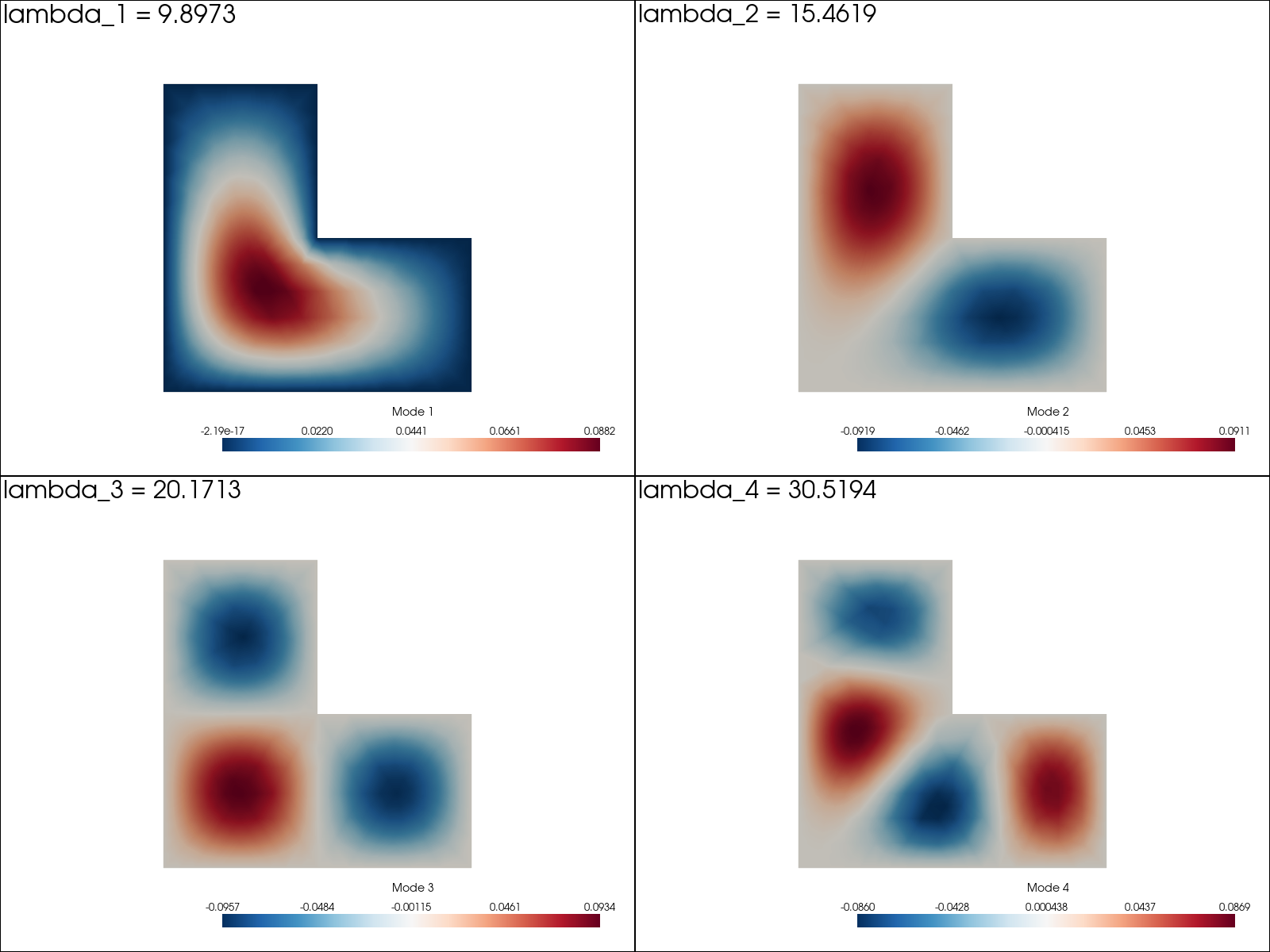
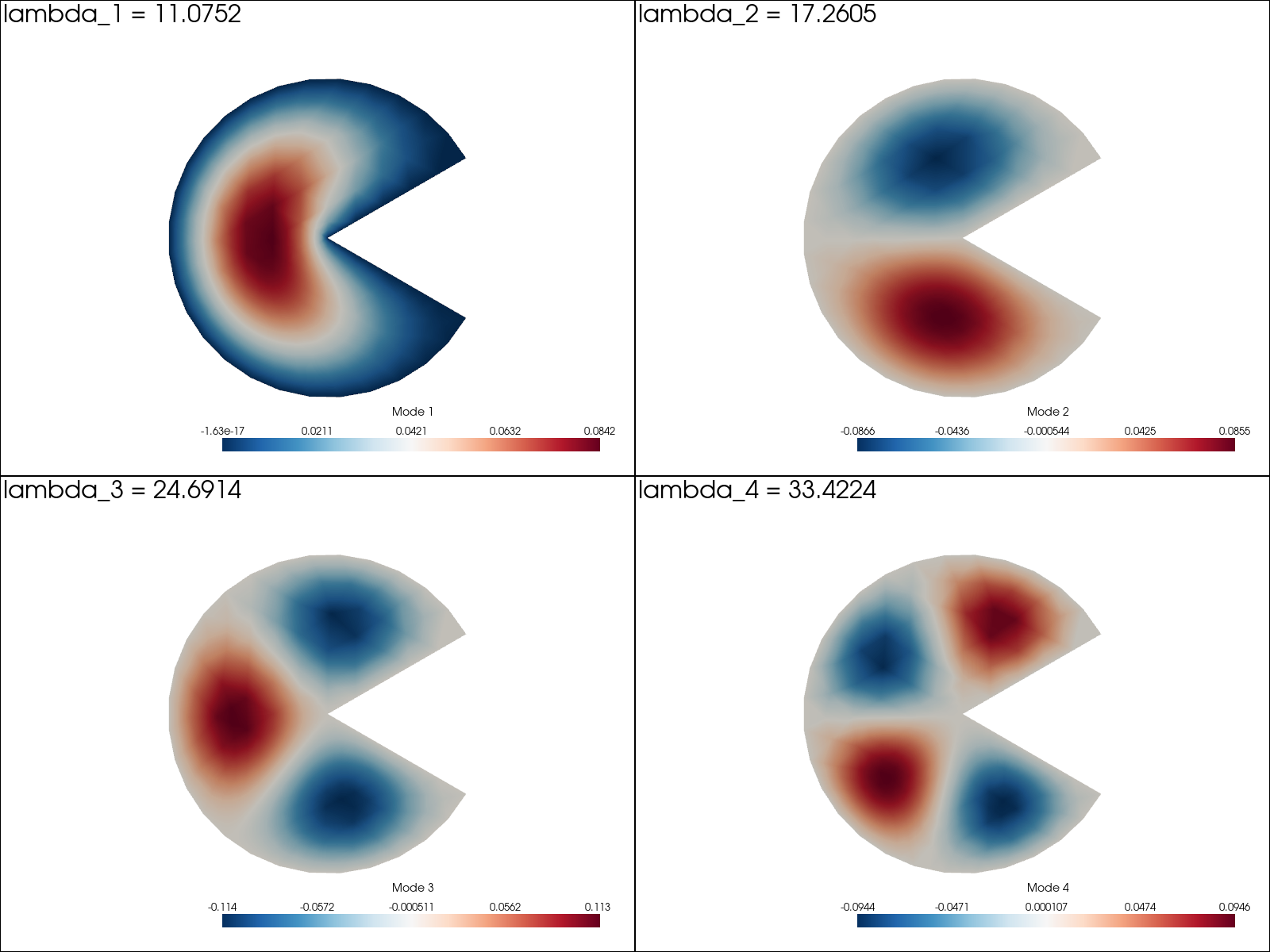
Author: Jørgen S. Dokken

Let us return to the Poisson problem and explore how to extend both the mathematical formulation and the implementation to handle a Dirichlet condition in combination with a Neumann condition. The domain is still the unit square, but this time we impose the Dirichlet condition u = u_D on the left and right boundaries, while the Neumann condition

\[-\frac{\partial u}{\partial n} = g\]

is applied to the remaining boundaries, \(y = 0\) and \(y = 1\)

The PDE problem

Let \(\Lambda_D\) and \(\Lambda_N\) denote the portions of the boundary \(\partial \Omega\) where the Dirichlet and Neumann conditions are prescribed, respectively The full boundary-value problem is then given by

\[ \begin{aligned} -\nabla^2 u &= f \quad \text{in } \Omega \\ u &= u_D \quad \text{on } \Lambda_D \\ -\frac{\partial u}{\partial n} &= g \quad \text{on } \Lambda_N \end{aligned} \]

As before, we choose \(u = 1 + x^2 + 2y^2\) as the exact solution and then set \(f\), \(g\), and \(u_D\) to match this choice

\[ \begin{aligned} f(x,y) &=-6 \\ g(x,y) &= \begin{cases} \phantom{-}0, & y=0\\ -4, & y=1 \end{cases}\\ u_D(x,y) &=1+x^2+2y^2 \end{aligned} \]

To simplify the implementation, we define \(g\) as a function over the whole domain , making sure it has the correct values at \(y=0\) and \(y=1\). One possible choice is

\[ g(x,y)=-4y \]

The variational formulation

The first step is to derive the variational formulation. In this case, the boundary term resulting from integration by parts cannot be omitted, since \(v\) vanishes only on \(\Lambda_D\). We obtain

\[-\int_\Omega (\nabla^2 u)\, v \,\mathrm{d}x \;=\; \int_\Omega \nabla u \cdot \nabla v \,\mathrm{d}x \;-\; \int_{\partial \Omega}\frac{\partial u}{\partial n} v \,\mathrm{d}s\]

and because \(v=0\) on \(\Lambda_D\), it follows that

\[-\int_{\partial \Omega}\frac{\partial u}{\partial n} v \,\mathrm{d}s \;=\; - \int_{\Lambda_N}\frac{\partial u}{\partial n} v \,\mathrm{d}s \;=\; \int_{\Lambda_N} g v \,\mathrm{d}s\]

by applying the boundary condition on \(\Lambda_N\). The resulting weak form is therefore

\[\int_\Omega \nabla u \cdot \nabla v \,\mathrm{d}x \;=\; \int_\Omega f v \,\mathrm{d}x \;-\; \int_{\Lambda_N} g v \,\mathrm{d}s\]

Expressing this equation in the standard notation \(a(u,v) = L(v)\), we have

\[\begin{aligned} a(u,v) &= \int_\Omega \nabla u \cdot \nabla v \,\mathrm{d}x \\ L(v) &= \int_\Omega f v \,\mathrm{d}x \;-\; \int_{\Lambda_N} g v \,\mathrm{d}s \end{aligned}\]

Implementation

As in the previous example, we start by defining the mesh, the function space, and the bilinear form \(a(u,v)\)

import numpy as np

from mpi4py import MPI
import pyvista

from dolfinx import default_scalar_type
from dolfinx.fem import (Constant, Function, functionspace,
  assemble_scalar, dirichletbc, form, locate_dofs_geometrical)
from dolfinx.fem.petsc import LinearProblem
from dolfinx.mesh import create_unit_square
from dolfinx.plot import vtk_mesh

from ufl import SpatialCoordinate, TestFunction, TrialFunction, dot, ds, dx, grad

mesh = create_unit_square(MPI.COMM_WORLD, 10, 10)

V = functionspace(mesh, ("Lagrange", 1))
u = TrialFunction(V)
v = TestFunction(V)

a = dot(grad(u), grad(v)) *dx

Now we turn to the Neumann and Dirichlet boundary conditions. As before, we use a Python function to mark the part of the boundary where the Dirichlet condition should apply. With this function, we can then identify the corresponding degrees of freedom that satisfy the condition

def u_exact(x):
  return 1 +x[0]**2 +2 *x[1]**2

def boundary_D(x):
  return np.logical_or(np.isclose(x[0], 0), np.isclose(x[0], 1))

dofs_D = locate_dofs_geometrical(V, boundary_D)

u_bc = Function(V)
u_bc.interpolate(u_exact)
bc = dirichletbc(u_bc, dofs_D)

The next step is to define the Neumann condition. We begin by defining \(g\) using UFL’s SpatialCoordinate function, and then create a boundary integration measure ds. Since the test function \(v\) vanishes on the Dirichlet boundary, the corresponding integrals drop out. This allows us to simply integrate g *v *ds over the entire boundary

f = Constant(mesh, default_scalar_type(-6))

x = SpatialCoordinate(mesh)
g = -4 *x[1]

L = f *v *dx -g *v *ds

At this stage, we are ready to assemble the linear system and solve it

problem = LinearProblem(
    a, 
    L, 
    bcs=[bc], 
    petsc_options={
        "ksp_type": "preonly", 
        "pc_type": "lu"}
)

uh = problem.solve()

V2 = functionspace(mesh, ("Lagrange", 2))
uex = Function(V2)
uex.interpolate(u_exact)

error_L2 = assemble_scalar(form((uh -uex)**2 *dx))
error_L2 = np.sqrt(MPI.COMM_WORLD.allreduce(error_L2, op=MPI.SUM))

u_vertex_values = uh.x.array

uex_1 = Function(V)
uex_1.interpolate(uex)
u_ex_vertex_values = uex_1.x.array

error_max = np.max(np.abs(u_vertex_values -u_ex_vertex_values))
error_max = MPI.COMM_WORLD.allreduce(error_max, op=MPI.MAX)

print(f"Error_L2 : {error_L2:.2e}")
print(f"Error_max : {error_max:.2e}")
Error_L2 : 5.27e-03
Error_max : 1.78e-15

Visualization

To visualize the solution, run the code either as a Python script with off_screen=True, or inside a Jupyter notebook with off_screen=False

from pathlib import Path

results_folder = Path("fenicsx/bcs_subdomains")
results_folder.mkdir(exist_ok=True, parents=True)

pyvista_cells, cell_types, geometry = vtk_mesh(V)
grid = pyvista.UnstructuredGrid(pyvista_cells, cell_types, geometry)
grid.point_data["u"] = uh.x.array
grid.set_active_scalars("u")

plotter = pyvista.Plotter(off_screen=False)
plotter.add_text("uh", position="upper_edge", font_size=14, color="black")
plotter.add_mesh(grid, show_edges=True)
plotter.view_xy()

if not pyvista.OFF_SCREEN:
    #plotter.show()
    plotter.export_html(results_folder/"neumann_dirichlet.html")
else:
    figure = plotter.screenshot(results_folder/"neumann_dirichlet.png")

K.8.2 Setting multiple Dirichlet condition

In the previous section, we applied the same Dirichlet condition to both the left and right boundaries using a single function. While this works, it is often more flexible to define separate boundary conditions for each side.

Let us consider a similar setup to the earlier example, but this time with distinct Dirichlet conditions on the left and right boundaries:

\[ \begin{aligned} -\nabla^2 u &= f \quad &&\text{in } \Omega \\ u &= u_L \quad &&\text{on } \Lambda_D^L \\ u &= u_R \quad &&\text{on } \Lambda_D^R \\ -\frac{\partial u}{\partial n} &= g \quad &&\text{on } \Lambda_N \end{aligned} \]

Here, \(\Lambda_D^L\) represents the left boundary (\(x=0\)), and \(\Lambda_D^R\) represents the right boundary (\(x=1\))

For this example, we choose

  • \(u_L(y) = 1 + 2y^2\)

  • \(u_R(y) = 2 + 2y^2\)

  • \(g(y) = -4y\)

in line with the analytical solution introduced earlier

As before, we begin by defining the mesh, the function space, and the variational formulation

import numpy as np
from mpi4py import MPI
import pyvista

from dolfinx import default_scalar_type
from dolfinx.fem import (
  Constant, Function, functionspace,
  assemble_scalar, dirichletbc, 
  form, locate_dofs_geometrical
)
from dolfinx.fem.petsc import LinearProblem
from dolfinx.mesh import create_unit_square
from dolfinx.plot import vtk_mesh

from ufl import (
  SpatialCoordinate, 
  TrialFunction, TestFunction, 
  dot, dx, ds, grad
)

def u_exact(x):
  return 1 +x[0]**2 +2 *x[1]**2

mesh = create_unit_square(MPI.COMM_WORLD, 10, 10)

V = functionspace(mesh, ("Lagrange", 1))
u = TrialFunction(V)
v = TestFunction(V)

a = dot(grad(u), grad(v)) *dx

x = SpatialCoordinate(mesh)
f = Constant(mesh, default_scalar_type(-6))
g = - 4 *x[1]
L = f *v *dx -g *v *ds

Our next step is to mark the two boundaries individually, beginning with the left boundary

dofs_L = locate_dofs_geometrical(V, lambda x: np.isclose(x[0], 0))
u_L = Function(V)
u_L.interpolate(lambda x: 1 +2 *x[1]**2)
bc_L = dirichletbc(u_L, dofs_L)

Note that we have used lambda-functions to compactly define the functions returning the subdomain evaluation and function evaluation. We can use a similar procedure for the right boundary condition, and gather both boundary conditions in a vector bcs

dofs_R = locate_dofs_geometrical(V, lambda x: np.isclose(x[0], 1))
u_R = Function(V)
u_R.interpolate(lambda x: 2 +2 *x[1]**2)
bc_R = dirichletbc(u_R, dofs_R)
bcs = [bc_R, bc_L]

We are now ready to solve the problem once more and evaluate both the \(L^2\) error and the maximum error at the mesh vertices

problem = LinearProblem(
  a, 
  L, 
  bcs=bcs, 
  petsc_options={"ksp_type": "preonly", "pc_type": "lu"}
)
uh = problem.solve()

V2 = functionspace(mesh, ("Lagrange", 2))
uex = Function(V2)
uex.interpolate(u_exact)

error_L2 = assemble_scalar(form((uh -uex)**2 *dx))
error_L2 = np.sqrt(MPI.COMM_WORLD.allreduce(error_L2, op=MPI.SUM))

u_vertex_values = uh.x.array
uex_1 = Function(V)
uex_1.interpolate(uex)
u_ex_vertex_values = uex_1.x.array

error_max = np.max(np.abs(u_vertex_values -u_ex_vertex_values))
error_max = MPI.COMM_WORLD.allreduce(error_max, op=MPI.MAX)

print(f"Error_L2 : {error_L2:.2e}")
print(f"Error_max : {error_max:.2e}")
Error_L2 : 5.27e-03
Error_max : 2.22e-15

Visualization

To visualize the solution, run the code either as a Python script with off_screen=True, or inside a Jupyter notebook with off_screen=False

from pathlib import Path

results_folder = Path("fenicsx/bcs_subdomains")
results_folder.mkdir(exist_ok=True, parents=True)

pyvista_cells, cell_types, geometry = vtk_mesh(V)
grid = pyvista.UnstructuredGrid(pyvista_cells, cell_types, geometry)
grid.point_data["u"] = uh.x.array
grid.set_active_scalars("u")

plotter = pyvista.Plotter(off_screen=False)
plotter.add_text("uh", position="upper_edge", font_size=14, color="black")
plotter.add_mesh(grid, show_edges=True)
plotter.view_xy()

if not pyvista.OFF_SCREEN:
    #plotter.show()
    plotter.export_html(results_folder/"multiple_dirichlet.html")
else:
    figure = plotter.screenshot(results_folder/"multiple_dirichlet.png")

K.8.3 Defining subdomains for different materials

Author: Jørgen S. Dokken

Many PDE problems involve domains consisting of different materials. In FEniCSx, these cases can be treated by introducing a discontinuous, cell-wise constant function. We can create such a function on any mesh in the following way

Subdomains on built-in meshes

import numpy as np
from mpi4py import MPI
import pyvista

import gmsh

from dolfinx import default_scalar_type
from dolfinx.mesh import create_unit_square, locate_entities
from dolfinx.fem import (
  Constant, dirichletbc, Function, functionspace, 
  assemble_scalar, form, 
  locate_dofs_geometrical, locate_dofs_topological
)
from dolfinx.fem.petsc import LinearProblem
from dolfinx.io import XDMFFile, gmshio
from dolfinx.plot import vtk_mesh

from ufl import (
  SpatialCoordinate, TestFunction, TrialFunction,
  dx, grad, inner
)

mesh = create_unit_square(MPI.COMM_WORLD, 10, 10)
Q = functionspace(mesh, ("DG", 0))

To illustrate the concept, let’s consider a simple two-dimensional example with two materials. The domain \(\Omega=[0,1]\times[0,1]\) is split into two subdomains, \(\Omega_1=[0,1]\times [0,1/2]\) and \(\Omega_2=[0,1]\times[1/2, 1]\). We start by defining two Python functions, where each function returns True whenever the given coordinate falls inside its corresponding subdomain

def Omega_1(x):
  return x[1] <= 0.5

def Omega_2(x):
  return x[1] >= 0.5

Notice that both functions make use of \(\leq\) and \(\geq\). This is because FEniCSx evaluates each cell at all of its vertices, and we need every vertex on the interface to return True in order for the interface to be marked correctly.

With this in place, we now move on to a variable-coefficient version of the Poisson equation:

\[\begin{aligned} -\nabla \cdot &[\kappa(x,y)\,\nabla u(x, y)] = 1 &&\text{in } \Omega \\[5pt] u &= u_D = 1 &&\text{on } \partial\Omega_D = {(0,y),|, y \in [0,1]} \\[5pt] -\frac{\partial u}{\partial n} &= 0 &&\text{on } \partial\Omega \setminus \partial\Omega_D \end{aligned} \]

The next step is to define the coefficient \(\kappa\)

kappa = Function(Q)
cells_1 = locate_entities(mesh, mesh.topology.dim, Omega_1)
cells_2 = locate_entities(mesh, mesh.topology.dim, Omega_2)

In the previous code block, we determined which cells (triangular elements) belong to \(\Omega_1\) and \(\Omega_2\). Since a DG-0 function has a single degree of freedom per cell, there is a one-to-one correspondence between the degrees of freedom and the cells. We then define the coefficient \(\kappa\) by

\[ \kappa = \begin{cases} \phantom{.}1 & \text{if } x \in \Omega_1 \\ 0.1 & \text{if } x \in \Omega_2 \end{cases}\]

kappa.x.array[cells_1] = np.full_like(cells_1, 1, dtype=default_scalar_type)
kappa.x.array[cells_2] = np.full_like(cells_2, 0.1, dtype=default_scalar_type)
# Filter out ghosted cells
tdim = mesh.topology.dim
num_cells_local = mesh.topology.index_map(tdim).size_local
marker = np.zeros(num_cells_local, dtype=np.int32)

cells_1 = cells_1[cells_1 < num_cells_local]
cells_2 = cells_2[cells_2 < num_cells_local]

marker[cells_1] = 1
marker[cells_2] = 2

mesh.topology.create_connectivity(tdim, tdim)
topology, cell_types, x = vtk_mesh(mesh, tdim, np.arange(num_cells_local, dtype=np.int32))
from pathlib import Path

results_folder = Path("fenicsx/bcs_subdomains")
results_folder.mkdir(exist_ok=True, parents=True)

plotter = pyvista.Plotter(off_screen=False, window_size=[800, 800])

grid = pyvista.UnstructuredGrid(topology, cell_types, x)
grid.cell_data["Marker"] = marker
grid.set_active_scalars("Marker")
plotter.add_mesh(grid, show_edges=True)

if not pyvista.OFF_SCREEN:
    #plotter.show()
    plotter.export_html(results_folder/"subdomains_structured.html")
else:
    figure = plotter.screenshot(results_folder/"subdomains_structured.png")

After performing integration by parts, we are now ready to define the variational formulation and the Dirichlet boundary condition

V = functionspace(mesh, ("Lagrange", 1))
u = TrialFunction(V)
v = TestFunction(V)

a = inner(kappa *grad(u), grad(v)) *dx

x = SpatialCoordinate(mesh)
L = Constant(mesh, default_scalar_type(1)) *v *dx

dofs = locate_dofs_geometrical(V, lambda x: np.isclose(x[0], 0))
bcs = [dirichletbc(default_scalar_type(1), dofs, V)]

We can now solve the problem and visualize its solution

problem = LinearProblem(
  a, 
  L, 
  bcs=bcs, 
  petsc_options={"ksp_type": "preonly", "pc_type": "lu"}
)
uh = problem.solve()
plotter = pyvista.Plotter(off_screen=False, window_size=[800, 800])
grid_uh = pyvista.UnstructuredGrid(*vtk_mesh(V))
grid_uh.point_data["u"] = uh.x.array.real
grid_uh.set_active_scalars("u")

plotter.add_mesh(grid_uh, show_edges=True)
if not pyvista.OFF_SCREEN:
  #plotter.show()
  plotter.export_html(results_folder/"subdomains_structured2.html")
else:
  figure = plotter.screenshot(results_folder/"subdomains_structured2.png")

Distinct behaviors are clearly observed in the two regions, despite both having the same Dirichlet boundary condition at x=0 on the left boundary

Interpolation with Python-function

As we saw in the first approach, in many cases the geometrical coordinates can be used to determine which coefficient to apply. Using the unstructured mesh from the previous example, we illustrate an alternative approach based on interpolation

def eval_kappa(x):
  values = np.zeros(x.shape[1], dtype=default_scalar_type)
  
  # Create a boolean array indicating which dofs 
  #   that are in each domain
  top_coords = x[1] > 0.5
  bottom_coords = x[1] < 0.5

  values[top_coords] = np.full(sum(top_coords), 0.1)
  values[bottom_coords] = np.full(sum(bottom_coords), 1)

  return values
kappa2 = Function(Q)
kappa2.interpolate(eval_kappa)

We verify this by computing the error between the new function and the previous one

# Difference in kappa's
error = mesh.comm.allreduce(assemble_scalar(form((kappa -kappa2)**2 *dx)))
print(f'{error = }')
error = 0.0

Subdomains defined from external mesh data

Let us now consider the same problem, but using GMSH to generate both the mesh and the subdomains. We will then show how to use this data to create discontinuous functions in dolfinx

gmsh.initialize()

proc = MPI.COMM_WORLD.rank

top_marker = 2
bottom_marker = 1
left_marker = 1

if proc == 0:
  # We create one rectangle for each subdomain
  gmsh.model.occ.addRectangle(0, 0, 0, 1, 0.5, tag=1)
  gmsh.model.occ.addRectangle(0, 0.5, 0, 1, 0.5, tag=2)
  # We fuse the two rectangles and keep the interface between them
  gmsh.model.occ.fragment([(2, 1)], [(2, 2)])
  gmsh.model.occ.synchronize()

  # Mark the top (2) and bottom (1) rectangle
  top, bottom = None, None
  for surface in gmsh.model.getEntities(dim=2):
    com = gmsh.model.occ.getCenterOfMass(surface[0], surface[1])
    if np.allclose(com, [0.5, 0.25, 0]):
      bottom = surface[1]
    else:
      top = surface[1]
  gmsh.model.addPhysicalGroup(2, [bottom], bottom_marker)
  gmsh.model.addPhysicalGroup(2, [top], top_marker)
  
  # Tag the left boundary
  left = []
  for line in gmsh.model.getEntities(dim=1):
    com = gmsh.model.occ.getCenterOfMass(line[0], line[1])
    if np.isclose(com[0], 0):
      left.append(line[1])
  gmsh.model.addPhysicalGroup(1, left, left_marker)
  
  gmsh.model.mesh.generate(2)
  gmsh.write(str(results_folder/"gmsh_mesh.msh"))

gmsh.finalize()
Info    : [  0%] Fragments                                                                                  Info    : [ 10%] Fragments                                                                                  Info    : [ 20%] Fragments                                                                                  Info    : [ 30%] Fragments                                                                                  Info    : [ 40%] Fragments                                                                                  Info    : [ 50%] Fragments                                                                                  Info    : [ 60%] Fragments                                                                                  Info    : [ 70%] Fragments                                                                                  Info    : [ 80%] Fragments - Splitting faces                                                                                                                                                                Info    : Meshing 1D...
Info    : [  0%] Meshing curve 1 (Line)
Info    : [ 20%] Meshing curve 2 (Line)
Info    : [ 30%] Meshing curve 3 (Line)
Info    : [ 50%] Meshing curve 4 (Line)
Info    : [ 60%] Meshing curve 5 (Line)
Info    : [ 80%] Meshing curve 6 (Line)
Info    : [ 90%] Meshing curve 7 (Line)
Info    : Done meshing 1D (Wall 0.000300625s, CPU 0.000553s)
Info    : Meshing 2D...
Info    : [  0%] Meshing surface 1 (Plane, Frontal-Delaunay)
Info    : [ 60%] Meshing surface 2 (Plane, Frontal-Delaunay)
Info    : Done meshing 2D (Wall 0.00269496s, CPU 0.004477s)
Info    : 101 nodes 214 elements
Info    : Writing 'fenicsx/bcs_subdomains/gmsh_mesh.msh'...
Info    : Done writing 'fenicsx/bcs_subdomains/gmsh_mesh.msh'

Read in MSH files with dolfinx

You can read MSH files with dolfinx, which initially loads them on a single process and then distributes them across the available ranks in the MPI communicator

mesh, cell_markers, facet_markers = gmshio.read_from_msh(
  results_folder/"gmsh_mesh.msh", 
  MPI.COMM_WORLD, 
  gdim=2
)
Info    : Reading 'fenicsx/bcs_subdomains/gmsh_mesh.msh'...
Info    : 15 entities
Info    : 101 nodes
Info    : 176 elements
Info    : Done reading 'fenicsx/bcs_subdomains/gmsh_mesh.msh'

Convert msh-files to XDMF using meshio

We will use meshio to read in the msh file, and convert it to a more suitable IO format. e start by creating a convenience function for extracting data for a single cell type, and creating a new meshio.Mesh

import meshio

def create_mesh(mesh, cell_type, prune_z=False):
  
  points = mesh.points[:, :2] if prune_z else mesh.points
  cells = mesh.get_cells_type(cell_type)
  cell_data = mesh.get_cell_data("gmsh:physical", cell_type)

  out_mesh = meshio.Mesh(
    points=points, 
    cells={cell_type: cells}, 
    cell_data={"name_to_read": [cell_data.astype(np.int32)]}
  )
  
  return out_mesh

This function returns a meshio mesh, including physical markers for the specified type. The prune_z argument is used when working with two-dimensional meshes. The last coordinate in the mesh (since it is generated in 3D space) must be removed for dolfinx to recognize it as a two-dimensional geometry

if proc == 0:
  # Read in mesh
  msh = meshio.read(results_folder/"gmsh_mesh.msh")

  # Create and save one file for the mesh, and one file for the facets
  triangle_mesh = create_mesh(msh, "triangle", prune_z=True)
  line_mesh = create_mesh(msh, "line", prune_z=True)
  meshio.write(results_folder/"mesh.xdmf", triangle_mesh)
  meshio.write(results_folder/"mt.xdmf", line_mesh)

MPI.COMM_WORLD.barrier()

We have written the mesh and cell markers to one file, and the facet markers to a separate file. This data can be read in dolfinx using XDMFFile.read_mesh and XDMFFile.read_meshtags. A dolfinx.MeshTags object stores the entity indices and their corresponding marker values in two one-dimensional arrays.

Note that the mesh was generated and written using a single processor. However, since the XDMF format supports parallel I/O, the mesh can be read in parallel

with XDMFFile(
  MPI.COMM_WORLD, 
  results_folder/"mesh.xdmf", "r"
) as xdmf:
  mesh = xdmf.read_mesh(name="Grid")
  ct = xdmf.read_meshtags(mesh, name="Grid")

mesh.topology.create_connectivity(mesh.topology.dim, mesh.topology.dim -1)

with XDMFFile(
  MPI.COMM_WORLD, 
  results_folder/"mt.xdmf", "r"
) as xdmf:
  ft = xdmf.read_meshtags(mesh, name="Grid")

Having read the mesh together with the associated cell and facet data, we can now construct the discontinuous function kappa as follows:

Q = functionspace(mesh, ("DG", 0))
kappa = Function(Q)

bottom_cells = ct.find(bottom_marker)
kappa.x.array[bottom_cells] = np.full_like(
  bottom_cells, 
  1, 
  dtype=default_scalar_type
)

top_cells = ct.find(top_marker)
kappa.x.array[top_cells] = np.full_like(
  top_cells, 
  0.1, 
  dtype=default_scalar_type
)

The facet data ft can also be used efficiently to construct the Dirichlet boundary condition.

V = functionspace(mesh, ("Lagrange", 1))
u_bc = Function(V)
left_facets = ft.find(left_marker)

mesh.topology.create_connectivity(mesh.topology.dim -1, mesh.topology.dim)
left_dofs = locate_dofs_topological(V, mesh.topology.dim -1, left_facets)

bcs = [dirichletbc(default_scalar_type(1), left_dofs, V)]

We can now solve the problem in a fashion similar to that used above

u = TrialFunction(V)
v = TestFunction(V)

a = inner(kappa *grad(u), grad(v)) *dx

x = SpatialCoordinate(mesh)
L = Constant(mesh, default_scalar_type(1)) *v *dx

problem = LinearProblem(
  a, 
  L, 
  bcs=bcs, 
  petsc_options={"ksp_type": "preonly", "pc_type": "lu"}
)
uh = problem.solve()
# Since dolfinx.MeshTag contains a value for every cell in the geometry, 
# we can attach it directly to the grid

tdim = mesh.topology.dim
mesh.topology.create_connectivity(tdim, tdim)

topology, cell_types, x = vtk_mesh(mesh, tdim)
grid = pyvista.UnstructuredGrid(topology, cell_types, x)

num_local_cells = mesh.topology.index_map(tdim).size_local
grid.cell_data["Marker"] = ct.values[ct.indices < num_local_cells]
grid.set_active_scalars("Marker")

plotter = pyvista.Plotter(off_screen=False, window_size=[800, 800])
plotter.add_mesh(grid, show_edges=True)

if not pyvista.OFF_SCREEN:
  #plotter.show()
  plotter.export_html(results_folder/"subdomains_unstructured.html")
else:
  figure = plotter.screenshot(results_folder/"subdomains_unstructured.png")
grid_uh = pyvista.UnstructuredGrid(*vtk_mesh(V))
grid_uh.point_data["u"] = uh.x.array.real
grid_uh.set_active_scalars("u")

plotter = pyvista.Plotter(off_screen=False, window_size=[800, 800])
plotter.add_mesh(grid_uh, show_edges=True)

if not pyvista.OFF_SCREEN:
  #plotter.show()
  plotter.export_html(results_folder/"subdomains_unstructured_u.html")
else:
  figure = plotter.screenshot(results_folder/"subdomains_unstructured_u.png")

K.8.4 Setting multiple Dirichlet, Neumann, and Robin conditions

Author: Hans Petter Langtangen and Anders Logg

We now look at the variable-coefficient example from the previous section. In this part, we will show how to apply a combination of Dirichlet, Neumann, and Robin boundary conditions to this problem

We split the boundary into three distinct parts:

  • \(\Gamma_D\) for Dirichlet conditions:

    \(\phantom{-\kappa\partial}u=u_D^i \quad\text{on } \Gamma_D^i \quad\) where \(\;\Gamma_D=\Gamma_D^0\cup \Gamma_D^1 \cup \dots\)

  • \(\Gamma_N\) for Neumann conditions:

    \(\displaystyle -\kappa \frac{\partial u}{\partial n}=g_j \quad\text{on } \Gamma_N^j \quad\) where \(\;\Gamma_N=\Gamma_N^0\cup \Gamma_N^1 \cup \dots\)

  • \(\Gamma_R\) for Robin conditions:

    \(\displaystyle -\kappa \frac{\partial u}{\partial n}=r_k (u -s_k) \quad\text{on } \Gamma_R^k \quad\) where \(\;\Gamma_R=\Gamma_R^0\cup \Gamma_R^1 \cup \dots\)

where \(r_k\) and \(s_k\) are prescribed functions. The Robin condition is commonly used to model heat transfer to the surroundings and arises naturally from Newton’s law of cooling. In this case, \(r_k\) represents the heat transfer coefficient, and \(s_k\) is the ambient temperature. Both may depend on space and time

The PDE problem and variational formulation

We can summarize the PDE problem as follows:

\[\begin{aligned} -\nabla &\cdot (\kappa \nabla u) = f &&\text{in } \Omega\\[6pt] u &= u_D^i \quad &&\text{on } \Gamma_D^i \\[5pt] -\kappa \frac{\partial u}{\partial n} &= g_j &&\text{on } \Gamma_N^j\\ -\kappa \frac{\partial u}{\partial n} &= r_k (u - s_k) &&\text{on } \Gamma_R^k \end{aligned}\]

As usual, we multiply the equation by a test function \(v\) and integrate by parts:

\[-\int_{\Omega} \nabla \cdot (\kappa \nabla u)\, v \,\mathrm{d}x = \int_{\Omega} \kappa \nabla u \cdot \nabla v \,\mathrm{d}x - \int_{\partial \Omega} \kappa \frac{\partial u}{\partial n} v \,\mathrm{d}s\]

On the Dirichlet part (\(\Gamma_D^i\)), the boundary integral vanishes since \(v = 0\). On the remaining parts of the boundary, we split the contributions into the Neumann boundaries (\(\Gamma_N^i\)) and the Robin boundaries (\(\Gamma_R^i\)). Inserting the boundary conditions, we obtain

\[-\int_{\partial\Omega} \kappa \frac{\partial u}{\partial n} v \,\mathrm{d}s = \sum_i \int_{\Gamma_N^i} g_i v \,\mathrm{d}s + \sum_i \int_{\Gamma_R^i} r_i (u - s_i) v \,\mathrm{d}s\]

Thus, the variational problem can be written as

\[\begin{aligned} F(u, v) &= \int_\Omega \kappa \nabla u \cdot \nabla v \,\mathrm{d}x + \sum_i \int_{\Gamma_N^i} g_i v \,\mathrm{d}s \\ &\quad + \sum_i \int_{\Gamma_R^i} r_i (u - s_i) v \,\mathrm{d}s - \int_\Omega f v \,\mathrm{d}x = 0 \end{aligned}\]

We are accustomed to writing the variational formulation in the form \(a(u, v) = L(v)\). This requires identifying the integrals that depend on the trial function \(u\) and collecting them in \(a(u, v)\), while the remaining terms form \(L(v)\). Note that the Robin condition contributes to both \(a(u, v)\) and \(L(v)\)

Thus, we have

\[a(u, v) = \int_{\Omega} \kappa \nabla u \cdot \nabla v \,\mathrm{d}x + \sum_i \int_{\Gamma_R^i} r_i \, u \, v \,\mathrm{d}s\]

\[L(v) = \int_{\Omega} f \, v \,\mathrm{d}x -\sum_i \int_{\Gamma_N^i} g_i \, v \,\mathrm{d}s +\sum_i \int_{\Gamma_R^i} r_i \, s_i \, v \,\mathrm{d}s\]

Implementation

First, we define the domain to be the unit square \([0,1] \times [0,1]\)

import numpy as np
from mpi4py import MPI
import pyvista

from dolfinx import default_scalar_type
from dolfinx.mesh import create_unit_square, locate_entities, meshtags
from dolfinx.fem import (
  Constant, Function, functionspace, assemble_scalar, 
  dirichletbc, form, locate_dofs_topological
)
from dolfinx.fem.petsc import LinearProblem
from dolfinx.io import XDMFFile
from dolfinx.plot import vtk_mesh

from ufl import (
  FacetNormal, Measure, SpatialCoordinate, 
  TestFunction, TrialFunction, 
  div, dot, dx, grad, inner, lhs, rhs
)

mesh = create_unit_square(MPI.COMM_WORLD, 10, 10)

In this section, we solve the Poisson problem for the manufactured solution

\[u_{ex} = 1 + x^2 + 2y^2\]

which gives \(\kappa = 1\) and \(f = -6\). The next step is to define the boundary condition parameters and specify where to apply them. In this example, we apply the following:

\[ \begin{aligned} \phantom{-\kappa} u &= u_D &&\quad \text{for } x=0,1\\[5pt] -\kappa \frac{\partial u}{\partial n} &= r(u - s) &&\quad \text{for } y=0\\ -\kappa \frac{\partial u}{\partial n} &= g_0 &&\quad \text{for } y=1 \end{aligned}\]

To reproduce the analytical solution, we set

\[ \begin{aligned} u_D &= u_{ex} = 1 + x^2 + 2y^2 \\ g_0 &= -\left.\frac{\partial u_{ex}}{\partial y}\right\vert_{y=1} = -4y \big\vert_{y=1} = -4 \end{aligned}\]

The Robin condition can be specified in many ways. Since

\[-\left.\frac{\partial u_{ex}}{\partial n}\right\vert_{y=0} = \left.\frac{\partial u_{ex}}{\partial y}\right\vert_{y=0} = 4y \big\vert_{y=0} = 0\]

we can choose \(r \neq 0\) arbitrarily and set \(s = u_{ex}\). Here, we choose \(r = 1000\)

We can now define all the necessary variables and assemble the traditional part of the variational form

x = SpatialCoordinate(mesh)
u_ex = lambda x: 1 +x[0]**2 +2*x[1]**2

# Define physical parameters and boundary condtions
kappa = Constant(mesh, default_scalar_type(1))

f = -div(grad(u_ex(x)))
n = FacetNormal(mesh)
g = -dot(n, grad(u_ex(x)))
s = u_ex(x)
r = Constant(mesh, default_scalar_type(1000))

# Define function space and standard part of variational form
V = functionspace(mesh, ("Lagrange", 1))
u = TrialFunction(V)
v = TestFunction(V)

F = kappa *inner(grad(u), grad(v)) *dx -inner(f, v) *dx

We begin by identifying the facets on each boundary and creating a custom integration measure, ds

boundaries = [
  (1, lambda x: np.isclose(x[0], 0)),
  (2, lambda x: np.isclose(x[0], 1)),
  (3, lambda x: np.isclose(x[1], 0)),
  (4, lambda x: np.isclose(x[1], 1))
]

Next, we go through each boundary condition and generate MeshTags that mark the corresponding facets

facet_indices, facet_markers = [], []
fdim = mesh.topology.dim -1

for (marker, locator) in boundaries:
  facets = locate_entities(mesh, fdim, locator)
  facet_indices.append(facets)
  facet_markers.append(np.full_like(facets, marker))

facet_indices = np.hstack(facet_indices).astype(np.int32)
facet_markers = np.hstack(facet_markers).astype(np.int32)
sorted_facets = np.argsort(facet_indices)

facet_tag = meshtags(
  mesh, 
  fdim, 
  facet_indices[sorted_facets], 
  facet_markers[sorted_facets]
)

Debugging boundary condition

A simple way to debug boundary conditions is to visualize the boundaries in ParaView. We do this by writing the MeshTags to a file, after which individual boundaries can be examined using the Threshold filter

from pathlib import Path

results_folder = Path("fenicsx/fundamentals")
results_folder.mkdir(exist_ok=True, parents=True)

mesh.topology.create_connectivity(mesh.topology.dim -1, mesh.topology.dim)
with XDMFFile(mesh.comm, results_folder/"facet_tags.xdmf", "w") as xdmf:
    xdmf.write_mesh(mesh)
    xdmf.write_meshtags(facet_tag, mesh.geometry)

Next, we define a custom integration measure, ds, which can be used to restrict integration to selected facets. Using ds(1) ensures that we integrate only over facets that have been assigned the value 1 in the corresponding facet_tag

ds = Measure("ds", domain=mesh, subdomain_data=facet_tag)

Next, we define a general boundary condition class that can handle different types of boundary conditions

class BoundaryCondition():
  def __init__(self, type, marker, values):
    self._type = type
    if type == "Dirichlet":
      u_D = Function(V)
      u_D.interpolate(values)
      facets = facet_tag.find(marker)
      dofs = locate_dofs_topological(V, fdim, facets)
      self._bc = dirichletbc(u_D, dofs)
    elif type == "Neumann":
      self._bc = inner(values, v) *ds(marker)
    elif type == "Robin":
      self._bc = values[0] *inner(u -values[1], v) *ds(marker)
    else:
      raise TypeError(f"Unknown boundary condition: {type:s}")
  
  @property
  def bc(self):
    return self._bc

  @property
  def type(self):
    return self._type

# Define the Dirichlet condition
boundary_conditions = [
  BoundaryCondition("Dirichlet", 1, u_ex),
  BoundaryCondition("Dirichlet", 2, u_ex),
  BoundaryCondition("Robin", 3, (r, s)),
  BoundaryCondition("Neumann", 4, g)
]

Next, we go through each boundary condition and add it to \(L(v)\) or include it in the list of Dirichlet boundary conditions, depending on its type

bcs = []
for condition in boundary_conditions:
  if condition.type == "Dirichlet":
    bcs.append(condition.bc)
  else:
    F += condition.bc

We can now create the bilinear form a and the linear form L using the ufl functions lhs and rhs

# Solve linear variational problem
a = lhs(F)
L = rhs(F)

problem = LinearProblem(
  a, 
  L, 
  bcs=bcs, 
  petsc_options={"ksp_type": "preonly", "pc_type": "lu"}
)
uh = problem.solve()
from pathlib import Path

results_folder = Path("fenicsx/bcs_subdomains")
results_folder.mkdir(exist_ok=True, parents=True)

# Visualize solution
pyvista_cells, cell_types, geometry = vtk_mesh(V)
grid = pyvista.UnstructuredGrid(pyvista_cells, cell_types, geometry)
grid.point_data["u"] = uh.x.array
grid.set_active_scalars("u")

plotter = pyvista.Plotter(off_screen=True)
plotter.add_text("uh", position="upper_edge", font_size=14, color="black")
plotter.add_mesh(grid, show_edges=True)
plotter.view_xy()

if not pyvista.OFF_SCREEN:
  #plotter.show()
  plotter.export_html(results_folder/"robin_neumann_dirichlet.html")
else:
  figure = plotter.screenshot(results_folder/"robin_neumann_dirichlet.png")

Verification

Following the approach used in the previous problems, we calculate the error of the computed solution and compare it to the analytical solution

# Compute L2 error and error at nodes
V_ex = functionspace(mesh, ("Lagrange", 2))
u_exact = Function(V_ex)
u_exact.interpolate(u_ex)

error_L2 = np.sqrt(
  mesh.comm.allreduce(
    assemble_scalar(form((uh -u_exact)**2 *dx)), 
    op=MPI.SUM
  )
)

u_vertex_values = uh.x.array
uex_1 = Function(V)
uex_1.interpolate(u_ex)
u_ex_vertex_values = uex_1.x.array

error_max = np.max(np.abs(u_vertex_values -u_ex_vertex_values))
error_max = mesh.comm.allreduce(error_max, op=MPI.MAX)

print(f"Error_L2 : {error_L2:.2e}")
print(f"Error_max : {error_max:.2e}")
Error_L2 : 4.86e-03
Error_max : 2.07e-03

K.8.5 Component-wise Dirichlet BC

Author: Jørgen S. Dokken

We consider the linear elasticity problem on the rectangular domain \(\Omega=[0,L]\times[0,H]\) with displacement \(u=(u_x,u_y)\). The strong form with the boundary conditions is

\[ \begin{aligned} -\,\nabla\cdot\sigma(u) &= f &&\quad\text{in }\Omega\\[2mm] u &= 0 &&\quad\text{on }\Gamma_D \;(\text{bottom } y=0)\\[2mm] u_x &= 0 &&\quad\text{on }\Gamma_{D_x} \;(\text{right } x=L) \\[2mm] \sigma(u)\cdot n &= 0 &&\quad\text{on }\Gamma_N \;(\text{left } x=0 \text{ and top } y=H) \end{aligned}\]

where the stress and strain are given by

\[\begin{aligned} \sigma(u) &= \lambda\,\mathrm{tr}(\epsilon(u))\,I + 2\mu\,\epsilon(u)\\[2mm] \epsilon(u) &= \tfrac{1}{2}\big(\nabla u + \nabla u^\top\big) \end{aligned}\]

Physical interpretation

  • \(\Gamma_D\) (bottom): The boundary is fully clamped, meaning both displacement components vanish

\[u = (u_x,u_y) = 0\]

  • \(\Gamma_{D_x}\) (right): Only the horizontal displacement is constrained \(u_x = 0\), while the vertical displacement \(u_y\) is left free

  • \(\Gamma_N\) (left and top): These boundaries are traction-free, that is,

\[\sigma(u)\cdot n = 0\]

The chosen combination of boundary conditions eliminates possible rigid body motions. This ensures that the variational problem admits a unique solution, i.e. the problem is well-posed

import numpy as np
from mpi4py import MPI
import pyvista

from dolfinx import default_scalar_type
from dolfinx.mesh import CellType, create_rectangle, locate_entities_boundary
from dolfinx.fem import (
  Constant, dirichletbc, Function, functionspace, 
  locate_dofs_geometrical, locate_dofs_topological
)
from dolfinx.fem.petsc import LinearProblem
from dolfinx.plot import vtk_mesh

from petsc4py import PETSc

from ufl import (
  Identity, Measure, TestFunction, TrialFunction, 
  dot, dx, inner, grad, nabla_div, sym
)

L = 1
H = 1.3

lambda_ = 1.25
mu = 1
rho = 1
g = 1

As in the previous demos, we begin by defining the computational mesh and the corresponding function space. The function space is chosen to represent vector-valued functions, since the unknown displacement field \(u = (u_x, u_y)\) has two components

mesh = create_rectangle(
    MPI.COMM_WORLD, 
    np.array([[0, 0], [L, H]]), 
    [30, 30], 
    cell_type=CellType.triangle
)
V = functionspace(mesh, ("Lagrange", 1, (mesh.geometry.dim,)))

Boundary conditions

Next, we define the boundary conditions for our problem

# Define geometric tolerance
tol = 1e-8

# Locate boundary facets
bottom_facets = locate_entities_boundary(
  mesh, 
  mesh.topology.dim -1,
  lambda x: np.isclose(x[1], 0.0, atol=tol)
)

right_facets = locate_entities_boundary(
  mesh, 
  mesh.topology.dim -1,
  lambda x: np.isclose(x[0], L, atol=tol)
)

# Define boundary conditions
u_bc = Function(V)

# Γ_D (bottom): u = (0,0)
bc_bottom = dirichletbc(
  PETSc.ScalarType((0.0, 0.0)), 
  locate_dofs_topological(V, mesh.topology.dim -1, bottom_facets), 
  V
)

# Γ_{Dx} (right): u_x = 0
bc_right_x = dirichletbc(
  PETSc.ScalarType(0.0),
  locate_dofs_topological(V.sub(0), mesh.topology.dim -1, right_facets),
  V.sub(0)
)

# Collect Dirichlet boundary conditions
bcs = [bc_bottom, bc_right_x]

Note that the traction-free boundaries \(\Gamma_N\) (left and top) do not require explicit constraints in the variational formulation, since they are naturally included through the weak form of the problem

Variational formulation

We now turn to the weak form of the elasticity problem. Multiplying the PDE by a test function \(v\) and integrating by parts yields the variational form

\[a(u,v) = L(v)\]

where

\[\begin{aligned} a(u,v) &= \int_\Omega \sigma(u):\epsilon(v) \,\mathrm{d}x \\ L(v) &= \int_\Omega f \cdot v \,\mathrm{d}x \end{aligned}\]

Note that the Neumann boundary conditions on \(\Gamma_N\) (traction-free boundaries) are naturally included in the weak formulation, and therefore do not need to be imposed explicitly

# Strain and stress
def epsilon(u):
  return sym(grad(u))

# linear problem: tr(epsilon(u)) = nabla_div(u)
def sigma(u):
  return lambda_ *nabla_div(u) *Identity(len(u)) + 2 *mu *epsilon(u)

# Body force
f = Constant(mesh, default_scalar_type((0, -rho *g)))

# Define trial and test functions
u = TrialFunction(V)
v = TestFunction(V)

# Bilinear form and linear form
a = inner(sigma(u), epsilon(v)) *dx
L = dot(f, v) *dx  # +dot(T, v) *ds

As in the previous demos, we now assemble the system matrix and right-hand side vector, and then use PETSc to solve the resulting variational problem

# Define linear problem using PETSc
problem = LinearProblem(
  a, 
  L, 
  bcs=bcs,
  petsc_options={
    "ksp_type": "preonly",
    "pc_type": "lu"
  }
)

# Solve the system
uh = problem.solve()

# Print solver information
PETSc.Sys.Print("Linear system solved.")
Linear system solved.

Visualization

from pathlib import Path

results_folder = Path("fenicsx/bcs_subdomains")
results_folder.mkdir(exist_ok=True, parents=True)

topology, cell_types, x = vtk_mesh(V)
grid = pyvista.UnstructuredGrid(topology, cell_types, x)

vals = np.zeros((x.shape[0], 3))
vals[:, :len(uh)] = uh.x.array.reshape((x.shape[0], len(uh)))
grid["u"] = vals

# Create plotter and pyvista grid
plotter = pyvista.Plotter(off_screen=False)

actor_0 = plotter.add_mesh(grid, style="wireframe", color="k")
warped = grid.warp_by_vector("u", factor=1.1)
actor_1 = plotter.add_mesh(warped, opacity=0.8)
plotter.view_xy()

if not pyvista.OFF_SCREEN:
  ##p.show()
  plotter.export_html(results_folder/"component.html")
else:
  fig_array = plotter.screenshot(results_folder/"component.png")

K.8.6 Electromagnetics example

Author: Hans Petter Langtangen, Anders Logg and Jørgen S. Dokken

In this example, we consider an iron cylinder with copper wires wound around it, as illustrated below

A static current of \(J = 1\,\text{A}\) flows through the copper wires. Our goal is to compute the magnetic field B in the iron cylinder, the copper wires, and the surrounding vacuum

To simplify the problem, we note that the cylinder extends far in the \(z\)-direction, so the field can be assumed to be independent of the \(z\)-coordinate. This reduces the problem to a two-dimensional cross-section in the \(x\)–\(y\) plane

We begin with Maxwell’s equations in magnetostatics:

\[\nabla \cdot \mathbf{B} = 0, \quad \nabla \times \mathbf{H} = \mathbf{J} \]

where \(\mathbf{B}\) is the magnetic flux density, \(\mathbf{H}\) is the magnetic field intensity, and \(\mathbf{J}\) is the current density. The constitutive relation connects \(\mathbf{B}\) and \(\mathbf{H}\):

\[\mathbf{B} = \mu \mathbf{H}\]

with \(\mu\) denoting the magnetic permeability of the medium

Step 1: Introducing the Vector Potential

Since \(\nabla \cdot \mathbf{B} = 0\), we may represent the magnetic flux density using a vector potential \(\mathbf{A}\):

\[\mathbf{B} = \nabla \times \mathbf{A}\]

Step 2: Substituting into Ampère’s Law

Using \(\mathbf{B} = \mu \mathbf{H}\), Ampère’s law becomes

\[\nabla \times \left(\frac{1}{\mu} \nabla \times \mathbf{A}\right) = \mathbf{J}\]

Step 3: Reduction to 2D

For a long cylinder aligned with the \(z\)-axis and a current flowing along \(z\), symmetry implies that the vector potential has only a \(z\)-component:

\[\mathbf{A}(x,y) = (0,0, A_z(x,y))\]

Thus, the magnetic flux density lies in the \(x\)-\(y\) plane

Step 4: Scalar Poisson Equation

With this reduction, the vector equation simplifies to a scalar Poisson equation for \(A_z\):

\[-\nabla \cdot \left(\frac{1}{\mu} \nabla A_z\right) = J_z\]

\[\lim_{\vert(x,y)\vert\to \infty}A_z = 0\]

where \(J_z\) is the \(z\)-component of the current density. Once \(A_z\) is known, the magnetic field can be recovered as

\[\mathbf{B} = \nabla \times \mathbf{A} = \left(\frac{\partial A_z}{\partial y}, \; -\frac{\partial A_z}{\partial x}, \; 0 \right)\]

Since we cannot compute on an infinite domain, we truncate the problem by surrounding the cylinder with a sufficiently large disk. On the boundary of this disk, we impose the condition \(A_z = 0\)

The current density \(J_z\) is prescribed inside the circular cross-sections of the copper wires. In the interior set of circles, we assign a current of \(+1\,\mathrm{A}\), while in the exterior set of circles, we assign a current of \(-1\,\mathrm{A}\). This ensures that the net current in the domain is balanced, making the problem well-posed and allowing for a consistent computation of the magnetic field throughout the iron, copper, and vacuum regions

Variational formulation

To derive the variational problem, we multiply the governing PDE by a test function \(v\) and integrate over the computational domain \(\Omega\):

\[-\int_\Omega \nabla \cdot \left( \mu^{-1} \nabla A_z \right) v \,\mathrm{d}x = \int_\Omega J_z v \,\mathrm{d}x\]

Applying integration by parts (Green’s theorem) gives

\[\int_\Omega \mu^{-1} \nabla A_z \cdot \nabla v \,\mathrm{d}x -\int_{\partial \Omega} \mu^{-1} \frac{\partial A_z}{\partial n} v \,\mathrm{d}s = \int_\Omega J_z v \,\mathrm{d}x\]

On the boundary \(\partial \Omega\), we have prescribed \(A_z = 0\), which implies that the test function \(v\) also vanishes there. Consequently, the boundary integral disappears, leaving us with the variational formulation:

\[a(A_z, v) = L(v)\]

where

\[ a(A_z, v) = \int_\Omega \mu^{-1} \nabla A_z \cdot \nabla v \,\mathrm{d}x, \qquad L(v) = \int_\Omega J_z v \,\mathrm{d}x\]

Thus, the problem reduces to finding \(A_z \in V\), where \(V\) is the appropriate function space with homogeneous Dirichlet boundary conditions, such that

\[a(A_z, v) = L(v) \quad \text{for all } v \in V\]

Meshing a complex structure with subdomains

We now turn to the practical implementation of the problem. The first step is to create the computational mesh. We can construct this geometry in GMSH. Each physical region (iron, copper wires, vacuum, and outer boundary) is tagged with unique markers. These markers are preserved when the mesh is imported into dolfinx, and they allow us to assign different material parameters and source terms

"""
Electromagnetic coil geometry generation using Gmsh and DOLFINx.
This script creates a 2D geometry consisting of:
- Iron cylinder (magnetic core)
- Copper wire windings (inner and outer)
- Vacuum/air background
"""

# Import required libraries
import numpy as np
from mpi4py import MPI

import gmsh
import pyvista

from dolfinx import default_scalar_type
from dolfinx.fem import (dirichletbc, Expression, Function, functionspace, 
                        locate_dofs_topological)
from dolfinx.fem.petsc import LinearProblem
from dolfinx.io import XDMFFile
from dolfinx.io.gmshio import model_to_mesh
from dolfinx.mesh import compute_midpoints, locate_entities_boundary
from dolfinx.plot import vtk_mesh

from ufl import TestFunction, TrialFunction, as_vector, dot, dx, grad, inner

# MPI configuration
rank = MPI.COMM_WORLD.rank

# Initialize Gmsh
gmsh.initialize()

# ============================================================================
# GEOMETRY PARAMETERS
# ============================================================================
R = 5      # Radius of computational domain

a = 1      # Inner radius of iron cylinder
b = 1.2    # Outer radius of iron cylinder

N = 8      # Number of copper wire windings
c_1 = 0.8  # Radius of inner copper wire circle
c_2 = 1.4  # Radius of outer copper wire circle
r = 0.1    # Radius of individual copper wires

# Mesh parameters
gdim = 2           # Geometric dimension (2D problem)
model_rank = 0     # MPI rank responsible for geometry creation
mesh_comm = MPI.COMM_WORLD

# ============================================================================
# GEOMETRY CREATION
# ============================================================================
if mesh_comm.rank == model_rank:

    # ------------------------------------------------------------------------
    # Create background domain (vacuum/air)
    # ------------------------------------------------------------------------
    print("Creating background domain...")
    background = gmsh.model.occ.addDisk(0, 0, 0, R, R)
    gmsh.model.occ.synchronize()    
    
    # ------------------------------------------------------------------------
    # Create iron cylinder (magnetic core)
    # ------------------------------------------------------------------------
    print("Creating iron cylinder geometry...")
    
    # Create outer and inner boundaries of iron cylinder
    outer_iron = gmsh.model.occ.addCircle(0, 0, 0, b)
    inner_iron = gmsh.model.occ.addCircle(0, 0, 0, a)
    
    # Create curve loops and surface for iron cylinder (annular region)
    gmsh.model.occ.addCurveLoop([outer_iron], 5)
    gmsh.model.occ.addCurveLoop([inner_iron], 6)
    iron = gmsh.model.occ.addPlaneSurface([5, 6])  # Surface with hole
    gmsh.model.occ.synchronize()

     # ------------------------------------------------------------------------
    # Create copper wire windings
    # ------------------------------------------------------------------------
    print(f"Creating {N} inner and {N} outer copper wire windings...")
    
    # Inner copper wires (North polarity) - evenly distributed
    angles_N = [i * 2 * np.pi / N for i in range(N)]
    wires_N = []
    for v in angles_N:
        x_pos = c_1 * np.cos(v)
        y_pos = c_1 * np.sin(v)
        wire = gmsh.model.occ.addDisk(x_pos, y_pos, 0, r, r)
        wires_N.append((2, wire))

    # Outer copper wires (South polarity) - offset by half angle
    angles_S = [(i + 0.5) * 2 * np.pi / N for i in range(N)]
    wires_S = []
    for v in angles_S:
        x_pos = c_2 * np.cos(v)
        y_pos = c_2 * np.sin(v)
        wire = gmsh.model.occ.addDisk(x_pos, y_pos, 0, r, r)
        wires_S.append((2, wire))
    
    gmsh.model.occ.synchronize()

    # ------------------------------------------------------------------------
    # Boolean operations to create final geometry
    # ------------------------------------------------------------------------
    print("Performing boolean operations...")
    
    # Combine all surfaces for fragmentation
    all_surfaces = [(2, iron)]
    all_surfaces.extend(wires_S)
    all_surfaces.extend(wires_N)
    
    # Fragment the background domain with all other surfaces
    # This creates non-overlapping regions
    whole_domain = gmsh.model.occ.fragment([(2, background)], all_surfaces)
    gmsh.model.occ.synchronize()

    # ------------------------------------------------------------------------
    # Assign physical markers to different regions
    # Physical markers are used for material properties:
    # - Tag 0: Vacuum/air background
    # - Tag 1: Iron cylinder
    # - Tags 2 to N+1: Inner copper wires
    # - Tags N+2 to 2*N+1: Outer copper wires
    # ------------------------------------------------------------------------
    print("Assigning physical markers...")
    
    inner_tag = 2
    outer_tag = 2 + N
    background_surfaces = []
    other_surfaces = []
    
    # Classify each surface based on geometric properties
    for domain in whole_domain[0]:
        # Get center of mass and total mass of the domain
        com = gmsh.model.occ.getCenterOfMass(domain[0], domain[1])
        mass = gmsh.model.occ.getMass(domain[0], domain[1])

        # Identify iron cylinder by its characteristic mass
        if np.isclose(mass, np.pi * (b**2 - a**2), rtol=1e-3):
            gmsh.model.addPhysicalGroup(domain[0], [domain[1]], tag=1)
            other_surfaces.append(domain)
            print(f"  Iron cylinder identified (tag=1)")        

        # Identify background surfaces by center of mass at origin
        elif np.allclose(com, [0, 0, 0], atol=1e-6):
            background_surfaces.append(domain[1])        
        
        # Identify inner copper wires by distance from origin
        elif np.isclose(np.linalg.norm(com), c_1, rtol=1e-3):
            gmsh.model.addPhysicalGroup(domain[0], [domain[1]], inner_tag)
            print(f"  Inner wire identified (tag={inner_tag})")
            inner_tag += 1
            other_surfaces.append(domain)
        
        # Identify outer copper wires by distance from origin
        elif np.isclose(np.linalg.norm(com), c_2, rtol=1e-3):
            gmsh.model.addPhysicalGroup(domain[0], [domain[1]], outer_tag)
            print(f"  Outer wire identified (tag={outer_tag})")
            outer_tag += 1
            other_surfaces.append(domain)
    
    # Assign physical marker for vacuum/air background
    gmsh.model.addPhysicalGroup(2, background_surfaces, tag=0)
    print(f"  Background/vacuum regions identified (tag=0)")

    # ------------------------------------------------------------------------
    # Configure adaptive mesh sizing
    # ------------------------------------------------------------------------
    print("Configuring mesh size fields...")
    
    # Create distance field from wire and iron boundaries
    gmsh.model.mesh.field.add("Distance", 1)
    edges = gmsh.model.getBoundary(other_surfaces, oriented=False)
    gmsh.model.mesh.field.setNumbers(1, "EdgesList", [e[1] for e in edges])
    
    # Create threshold field for adaptive sizing
    gmsh.model.mesh.field.add("Threshold", 2)
    gmsh.model.mesh.field.setNumber(2, "IField", 1)
    gmsh.model.mesh.field.setNumber(2, "LcMin", r / 3)    # Fine mesh near wires
    gmsh.model.mesh.field.setNumber(2, "LcMax", 6 * r)    # Coarse mesh far away
    gmsh.model.mesh.field.setNumber(2, "DistMin", 4 * r)  # Distance for fine mesh
    gmsh.model.mesh.field.setNumber(2, "DistMax", 10 * r) # Distance for coarse mesh
    
    # Set minimum field as background mesh
    gmsh.model.mesh.field.add("Min", 5)
    gmsh.model.mesh.field.setNumbers(5, "FieldsList", [2])
    gmsh.model.mesh.field.setAsBackgroundMesh(5)

    # ------------------------------------------------------------------------
    # Generate and optimize mesh
    # ------------------------------------------------------------------------
    print("Generating mesh...")
    
    # Use Frontal-Delaunay algorithm for 2D meshing
    gmsh.option.setNumber("Mesh.Algorithm", 7)
    
    # Generate 2D mesh
    gmsh.model.mesh.generate(gdim)
    
    # Optimize mesh quality using Netgen optimizer
    print("Optimizing mesh quality...")
    gmsh.model.mesh.optimize("Netgen")
    
    print("Geometry and mesh generation completed successfully!")

# Note: After this point, you would typically:
# 1. Convert the Gmsh model to DOLFINx mesh using model_to_mesh()
# 2. Set up the electromagnetic problem (Maxwell's equations)
# 3. Apply boundary conditions
# 4. Solve the finite element problem
Creating background domain...
Creating iron cylinder geometry...
Creating 8 inner and 8 outer copper wire windings...
Performing boolean operations...
Info    : [  0%] Fragments                                                                                  Info    : [ 10%] Fragments                                                                                  Info    : [ 20%] Fragments                                                                                  Info    : [ 30%] Fragments                                                                                  Info    : [ 40%] Fragments                                                                                  Info    : [ 70%] Fragments                                                                                  Info    : [ 80%] Fragments - Making faces                                                                                Info    : [ 90%] Fragments - Adding holes                                                                                Assigning physical markers...
  Iron cylinder identified (tag=1)
  Outer wire identified (tag=10)
  Outer wire identified (tag=11)
  Outer wire identified (tag=12)
  Outer wire identified (tag=13)
  Outer wire identified (tag=14)
  Outer wire identified (tag=15)
  Outer wire identified (tag=16)
  Outer wire identified (tag=17)
  Inner wire identified (tag=2)
  Inner wire identified (tag=3)
  Inner wire identified (tag=4)
  Inner wire identified (tag=5)
  Inner wire identified (tag=6)
  Inner wire identified (tag=7)
  Inner wire identified (tag=8)
  Inner wire identified (tag=9)
  Background/vacuum regions identified (tag=0)
Configuring mesh size fields...
Generating mesh...
Info    : Meshing 1D...
Info    : [  0%] Meshing curve 1 (Ellipse)
Info    : [ 10%] Meshing curve 2 (Ellipse)
Info    : [ 20%] Meshing curve 3 (Ellipse)
Info    : [ 20%] Meshing curve 4 (Ellipse)
Info    : [ 30%] Meshing curve 5 (Ellipse)
Info    : [ 30%] Meshing curve 6 (Ellipse)
Info    : [ 40%] Meshing curve 7 (Ellipse)
Info    : [ 40%] Meshing curve 8 (Circle)
Info    : [ 50%] Meshing curve 9 (Ellipse)
Info    : [ 50%] Meshing curve 10 (Ellipse)
Info    : [ 60%] Meshing curve 11 (Circle)
Info    : [ 60%] Meshing curve 12 (Ellipse)
Info    : [ 70%] Meshing curve 13 (Ellipse)
Info    : [ 70%] Meshing curve 14 (Ellipse)
Info    : [ 80%] Meshing curve 15 (Ellipse)
Info    : [ 80%] Meshing curve 16 (Ellipse)
Info    : [ 90%] Meshing curve 17 (Ellipse)
Info    : [ 90%] Meshing curve 18 (Ellipse)
Info    : [100%] Meshing curve 19 (Ellipse)
Info    : Done meshing 1D (Wall 0.00666967s, CPU 0.010754s)
Info    : Meshing 2D...
Info    : [  0%] Meshing surface 2 (Plane, Bamg)
Info    : [  0%] BAMG succeeded 1668 vertices 2920 triangles
Info    : [ 10%] Meshing surface 3 (Plane, Bamg)
Info    : [ 10%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 10%] BAMG succeeded 46 vertices 71 triangles
Info    : [ 10%] BAMG succeeded 46 vertices 71 triangles
Info    : [ 20%] Meshing surface 4 (Plane, Bamg)
Info    : [ 20%] BAMG succeeded 48 vertices 75 triangles
Info    : [ 20%] BAMG succeeded 48 vertices 75 triangles
Info    : [ 20%] Meshing surface 5 (Plane, Bamg)
Info    : [ 20%] BAMG succeeded 50 vertices 79 triangles
Info    : [ 20%] BAMG succeeded 48 vertices 75 triangles
Info    : [ 20%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 20%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 30%] Meshing surface 6 (Plane, Bamg)
Info    : [ 30%] BAMG succeeded 46 vertices 71 triangles
Info    : [ 30%] Meshing surface 7 (Plane, Bamg)
Info    : [ 30%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 30%] BAMG succeeded 46 vertices 71 triangles
Info    : [ 30%] BAMG succeeded 45 vertices 69 triangles
Info    : [ 30%] BAMG succeeded 45 vertices 69 triangles
Info    : [ 40%] Meshing surface 8 (Plane, Bamg)
Info    : [ 40%] BAMG succeeded 48 vertices 75 triangles
Info    : [ 40%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 40%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 40%] Meshing surface 9 (Plane, Bamg)
Info    : [ 40%] BAMG succeeded 45 vertices 69 triangles
Info    : [ 50%] Meshing surface 10 (Plane, Bamg)
Info    : [ 50%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 50%] BAMG succeeded 46 vertices 71 triangles
Info    : [ 50%] BAMG succeeded 46 vertices 71 triangles
Info    : [ 50%] Meshing surface 11 (Plane, Bamg)
Info    : [ 50%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 50%] BAMG succeeded 46 vertices 71 triangles
Info    : [ 50%] BAMG succeeded 46 vertices 71 triangles
Info    : [ 60%] Meshing surface 12 (Plane, Bamg)
Info    : [ 60%] BAMG succeeded 48 vertices 75 triangles
Info    : [ 60%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 60%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 60%] Meshing surface 13 (Plane, Bamg)
Info    : [ 60%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 60%] BAMG succeeded 46 vertices 71 triangles
Info    : [ 60%] BAMG succeeded 46 vertices 71 triangles
Info    : [ 70%] Meshing surface 14 (Plane, Bamg)
Info    : [ 70%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 70%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 70%] Meshing surface 15 (Plane, Bamg)
Info    : [ 70%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 70%] BAMG succeeded 46 vertices 71 triangles
Info    : [ 70%] BAMG succeeded 45 vertices 69 triangles
Info    : [ 70%] BAMG succeeded 45 vertices 69 triangles
Info    : [ 80%] Meshing surface 16 (Plane, Bamg)
Info    : [ 80%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 80%] BAMG succeeded 46 vertices 71 triangles
Info    : [ 80%] BAMG succeeded 46 vertices 71 triangles
Info    : [ 80%] Meshing surface 17 (Plane, Bamg)
Info    : [ 80%] BAMG succeeded 48 vertices 75 triangles
Info    : [ 80%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 80%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 90%] Meshing surface 18 (Plane, Bamg)
Info    : [ 90%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 90%] BAMG succeeded 47 vertices 73 triangles
Info    : [ 90%] Meshing surface 19 (Plane, Bamg)
Info    : [ 90%] BAMG succeeded 5933 vertices 11450 triangles
Info    : [ 90%] BAMG succeeded 5986 vertices 11556 triangles
Info    : [100%] Meshing surface 20 (Plane, Bamg)
Info    : [100%] BAMG succeeded 3287 vertices 6247 triangles
Info    : [100%] BAMG succeeded 3207 vertices 6087 triangles
Info    : [100%] BAMG succeeded 3197 vertices 6067 triangles
Info    : Done meshing 2D (Wall 2.12535s, CPU 3.12165s)
Info    : 10872 nodes 22481 elements
Optimizing mesh quality...
Info    : Optimizing mesh (Netgen)...
Info    : Done optimizing mesh (Wall 1.41701e-06s, CPU 1e-06s)
Geometry and mesh generation completed successfully!

Following the Navier–Stokes tutorial, we load the mesh directly into DOLFINx without first writing it to a file

mesh, ct, _ = model_to_mesh(gmsh.model, mesh_comm, model_rank, gdim=2)
gmsh.finalize()

To inspect the mesh, we use ParaView and obtain the following result

from pathlib import Path

results_folder = Path("fenicsx/bcs_subdomains")
results_folder.mkdir(exist_ok=True, parents=True)

with XDMFFile(MPI.COMM_WORLD, results_folder/"mt_electro.xdmf", "w") as xdmf:
    xdmf.write_mesh(mesh)
    xdmf.write_meshtags(ct, mesh.geometry)

We can also visualize the subdomains using PyVista

plotter = pyvista.Plotter(off_screen=False)

tdim = mesh.topology.dim
mesh.topology.create_connectivity(tdim, tdim)
num_local_cells = mesh.topology.index_map(tdim).size_local

grid = pyvista.UnstructuredGrid(*vtk_mesh(mesh, tdim))
grid.cell_data["Marker"] = ct.values[ct.indices < num_local_cells]
grid.set_active_scalars("Marker")

actor = plotter.add_mesh(grid, show_edges=True)
plotter.view_xy()

if not pyvista.OFF_SCREEN:
    #plotter.show()
    plotter.export_html(results_folder/"cell_tags.html")    
else:
    cell_tag_fig = plotter.screenshot(results_folder/"cell_tags.png")

Next, we define discontinuous functions for permeability \(\mu\) and current \(J_z\), based on the MeshTags as in “Defining subdomains for different materials”

"""
Material properties and current density setup for electromagnetic simulation.
This code assigns material properties (permeability) and current densities 
to different regions of the electromagnetic coil geometry.
"""

# ============================================================================
# MATERIAL PROPERTIES AND CURRENT DENSITY SETUP
# ============================================================================

def setup_material_properties(mesh, ct, N):
    """
    Set up material properties and current densities for electromagnetic simulation.
    
    Parameters:
    -----------
    mesh : dolfinx.mesh.Mesh
        The computational mesh
    ct : dolfinx.mesh.MeshTags
        Cell tags identifying different material regions
    N : int
        Number of copper wire windings
        
    Returns:
    --------
    mu : dolfinx.fem.Function
        Magnetic permeability function
    J : dolfinx.fem.Function
        Current density function
    """
    
    # Create discontinuous Galerkin function space (piecewise constant)
    # DG(0) is appropriate for material properties that are constant within each element
    Q = functionspace(mesh, ("DG", 0))
    
    # Get unique material tags from the mesh
    material_tags = np.unique(ct.values)
    print(f"Found material tags: {material_tags}")
    
    # Initialize functions for magnetic permeability and current density
    mu = Function(Q)  # Magnetic permeability [H/m]
    J = Function(Q)   # Current density [A/m²]
    
    # Initialize current density to zero everywhere
    # (only copper wires will have non-zero current)
    J.x.array[:] = 0.0
    
    print("Assigning material properties...")
    
    # ------------------------------------------------------------------------
    # MATERIAL PROPERTY DEFINITIONS
    # ------------------------------------------------------------------------
    
    # Physical constants and material properties
    mu_0 = 4 * np.pi * 1e-7        # Vacuum permeability [H/m]
    mu_copper = 1.26e-6            # Copper permeability ≈ μ₀ [H/m]
    mu_iron = 1e-5                 # Iron permeability (simplified) [H/m]
                                   # Note: Real iron μ ≈ 6.3e-3, but using 1e-5 here
    
    # Current density magnitude [A/m²]
    current_density_positive = 1.0   # Inner wires (North polarity)
    current_density_negative = -1.0  # Outer wires (South polarity)
    
    # ------------------------------------------------------------------------
    # ASSIGN PROPERTIES TO EACH MATERIAL REGION
    # ------------------------------------------------------------------------
    
    for tag in material_tags:
        # Find all cells belonging to this material tag
        cells = ct.find(tag)
        num_cells = len(cells)
        
        # Assign magnetic permeability based on material type
        if tag == 0:
            # Vacuum/air background
            mu_value = mu_0
            material_name = "Vacuum/Air"
            
        elif tag == 1:
            # Iron cylinder (magnetic core)
            mu_value = mu_iron
            material_name = "Iron"
            
        else:
            # Copper wires (both inner and outer)
            mu_value = mu_copper
            material_name = "Copper"
        
        # Set permeability values for all cells in this region
        mu.x.array[cells] = np.full_like(cells, mu_value, dtype=default_scalar_type)
        
        # ------------------------------------------------------------------------
        # ASSIGN CURRENT DENSITIES TO COPPER WIRES
        # ------------------------------------------------------------------------
        
        # Inner copper wires (tags 2 to N+1) - positive current (North polarity)
        if tag in range(2, 2 + N):
            J.x.array[cells] = np.full_like(cells, current_density_positive, 
                                          dtype=default_scalar_type)
            current_info = f" | J = +{current_density_positive} A/m²"
            
        # Outer copper wires (tags N+2 to 2N+1) - negative current (South polarity)
        elif tag in range(2 + N, 2 * N + 2):
            J.x.array[cells] = np.full_like(cells, current_density_negative, 
                                          dtype=default_scalar_type)
            current_info = f" | J = {current_density_negative} A/m²"
            
        else:
            # Non-conducting materials (vacuum, iron)
            current_info = " | J = 0 A/m²"
        
        # Print material assignment summary
        print(f"  Tag {tag:2d}: {material_name:10s} "
              f"| μ = {mu_value:.2e} H/m{current_info} "
              f"| {num_cells:4d} cells")
    
    print("Material properties assignment completed.")
    
    return mu, J

# ============================================================================
# USAGE EXAMPLE
# ============================================================================

# Assuming mesh, ct, and N are already defined from the geometry creation
mu, J = setup_material_properties(mesh, ct, N)
Found material tags: [ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17]
Assigning material properties...
  Tag  0: Vacuum/Air | μ = 1.26e-06 H/m | J = 0 A/m² | 17623 cells
  Tag  1: Iron       | μ = 1.00e-05 H/m | J = 0 A/m² | 2920 cells
  Tag  2: Copper     | μ = 1.26e-06 H/m | J = +1.0 A/m² |   71 cells
  Tag  3: Copper     | μ = 1.26e-06 H/m | J = +1.0 A/m² |   75 cells
  Tag  4: Copper     | μ = 1.26e-06 H/m | J = +1.0 A/m² |   73 cells
  Tag  5: Copper     | μ = 1.26e-06 H/m | J = +1.0 A/m² |   71 cells
  Tag  6: Copper     | μ = 1.26e-06 H/m | J = +1.0 A/m² |   69 cells
  Tag  7: Copper     | μ = 1.26e-06 H/m | J = +1.0 A/m² |   73 cells
  Tag  8: Copper     | μ = 1.26e-06 H/m | J = +1.0 A/m² |   69 cells
  Tag  9: Copper     | μ = 1.26e-06 H/m | J = +1.0 A/m² |   71 cells
  Tag 10: Copper     | μ = 1.26e-06 H/m | J = -1.0 A/m² |   71 cells
  Tag 11: Copper     | μ = 1.26e-06 H/m | J = -1.0 A/m² |   73 cells
  Tag 12: Copper     | μ = 1.26e-06 H/m | J = -1.0 A/m² |   71 cells
  Tag 13: Copper     | μ = 1.26e-06 H/m | J = -1.0 A/m² |   73 cells
  Tag 14: Copper     | μ = 1.26e-06 H/m | J = -1.0 A/m² |   69 cells
  Tag 15: Copper     | μ = 1.26e-06 H/m | J = -1.0 A/m² |   71 cells
  Tag 16: Copper     | μ = 1.26e-06 H/m | J = -1.0 A/m² |   73 cells
  Tag 17: Copper     | μ = 1.26e-06 H/m | J = -1.0 A/m² |   73 cells
Material properties assignment completed.

In the code above, a slightly less extreme value for the magnetic permeability of iron was chosen to make the solution more illustrative; otherwise, the field in the iron cylinder would dominate completely.

We now proceed to define the weak problem

"""
Finite Element Formulation for 2D Electromagnetic Problem (Magnetostatic).
This code sets up the weak form for solving ∇×(1/μ ∇×A) = J
where A is the magnetic vector potential (z-component only in 2D)
"""

def setup_electromagnetic_problem(mesh, mu, J):
    """
    Set up finite element formulation for 2D magnetostatic problem.
    
    Parameters:
    -----------
    mesh : dolfinx.mesh.Mesh
        Computational mesh
    mu : dolfinx.fem.Function  
        Magnetic permeability function
    J : dolfinx.fem.Function
        Current density function
        
    Returns:
    --------
    a : ufl.Form
        Bilinear form (left-hand side)
    L : ufl.Form  
        Linear form (right-hand side)
    bc : dolfinx.fem.DirichletBC
        Boundary condition
    V : dolfinx.fem.FunctionSpace
        Function space
    """
    
    print("Setting up finite element formulation...")
    
    # ------------------------------------------------------------------------
    # Function Space Definition
    # ------------------------------------------------------------------------
    # Use first-order Lagrange elements (P1) for magnetic vector potential
    # In 2D, we solve for A_z component only (out-of-plane)
    V = functionspace(mesh, ("Lagrange", 1))
    
    print(f"Function space: P1 Lagrange elements")
    print(f"Total DOFs: {V.dofmap.index_map.size_global}")
    
    # ------------------------------------------------------------------------
    # Boundary Conditions
    # ------------------------------------------------------------------------
    # Apply homogeneous Dirichlet BC: A_z = 0 on entire boundary
    # This assumes the magnetic vector potential vanishes at far-field
    
    # Get topological dimension for boundary identification
    tdim = mesh.topology.dim  # Should be 2 for 2D problem
    
    # Locate all boundary facets (edges in 2D, faces in 3D)
    # The lambda function returns True for all boundary points
    facets = locate_entities_boundary(mesh, tdim - 1, 
                                    lambda x: np.full(x.shape[1], True))
    
    # Find degrees of freedom on boundary facets
    dofs = locate_dofs_topological(V, tdim - 1, facets)
    
    # Create homogeneous Dirichlet boundary condition: A_z = 0
    bc = dirichletbc(default_scalar_type(0), dofs, V)
    
    print(f"Boundary condition: A_z = 0 on {len(facets)} boundary facets")
    print(f"Constrained DOFs: {len(dofs)}")
    
    # ------------------------------------------------------------------------
    # Weak Form Definition
    # ------------------------------------------------------------------------
    # Define trial and test functions
    u = TrialFunction(V)  # Trial function (A_z)
    v = TestFunction(V)   # Test function
    
    # Bilinear form: a(u,v) = ∫ (1/μ) ∇u · ∇v dx
    # This comes from the weak form of ∇×(1/μ ∇×A) = J
    # In 2D: ∇×A = (∂A_z/∂y, -∂A_z/∂x), so |∇×A|² = |∇A_z|²
    a = (1 / mu) * dot(grad(u), grad(v)) * dx
    
    # Linear form: L(v) = ∫ J·v dx  
    # Current density source term
    L = J * v * dx
    
    print("Weak form successfully defined:")
    print("  Bilinear form: a(u,v) = ∫ (1/μ) ∇u·∇v dx")
    print("  Linear form:   L(v)   = ∫ J v dx")
    print("  Boundary condition: u = 0 on ∂Ω")
    
    return a, L, bc, V

a, L, bc, V = setup_electromagnetic_problem(mesh, mu, J)    
Setting up finite element formulation...
Function space: P1 Lagrange elements
Total DOFs: 10872
Boundary condition: A_z = 0 on 53 boundary facets
Constrained DOFs: 53
Weak form successfully defined:
  Bilinear form: a(u,v) = ∫ (1/μ) ∇u·∇v dx
  Linear form:   L(v)   = ∫ J v dx
  Boundary condition: u = 0 on ∂Ω

We are now ready to solve the linear problem

def solve_electromagnetic_enhanced(V, a, L, bc, solver_options=None):
    """
    Enhanced solver with better control and monitoring.
    """
    
    print("Setting up enhanced electromagnetic solver...")
    
    # Create solution function
    A_z = Function(V)
    A_z.name = "MagneticVectorPotential"  # For visualization
    
    # Default solver options
    if solver_options is None:
        solver_options = {
            "ksp_type": "cg",           # Conjugate Gradient
            "pc_type": "hypre",         # Hypre preconditioner  
            "ksp_rtol": 1e-8,           # Relative tolerance
            "ksp_atol": 1e-12,          # Absolute tolerance
            "ksp_max_it": 1000,         # Maximum iterations
            "ksp_monitor": None,        # Monitor convergence
        }
    
    # Create linear problem with custom options
    problem = LinearProblem(
        a, L, 
        u=A_z, 
        bcs=[bc],
        petsc_options=solver_options
    )
    
    print("Solver configuration:")
    print(f"  Method: {solver_options.get('ksp_type', 'default')}")
    print(f"  Preconditioner: {solver_options.get('pc_type', 'default')}")
    print(f"  Tolerance: {solver_options.get('ksp_rtol', 'default')}")
    
    # Solve with timing
    import time
    start_time = time.time()
    
    try:
        problem.solve()
        solve_time = time.time() -start_time
        
        print("✅ Solution completed successfully!")
        print(f"  Solve time: {solve_time:.3f} seconds")
        print(f"  Solution range: [{A_z.x.array.min():.6e}, {A_z.x.array.max():.6e}]")
        print(f"  Solution norm: {np.linalg.norm(A_z.x.array):.6e}")
        
        # Check for reasonable solution
        if np.all(np.abs(A_z.x.array) < 1e-15):
            print("⚠️  WARNING: Solution is nearly zero - check source terms and materials")
            
    except Exception as e:
        print(f"❌ Solver failed: {e}")
        raise
    
    return A_z

A_z = solve_electromagnetic_enhanced(V, a, L, bc)
Setting up enhanced electromagnetic solver...
Solver configuration:
  Method: cg
  Preconditioner: hypre
  Tolerance: 1e-08
  Residual norms for dolfinx_solve_13803687728 solve.
  0 KSP Residual norm 3.613699164749e-06
  1 KSP Residual norm 3.166937502590e-07
  2 KSP Residual norm 1.863176484264e-08
  3 KSP Residual norm 7.705910828606e-10
  4 KSP Residual norm 7.372646673478e-11
  5 KSP Residual norm 5.798240763766e-12
  6 KSP Residual norm 4.548044179577e-13
✅ Solution completed successfully!
  Solve time: 0.037 seconds
  Solution range: [-7.260387e-09, 9.400186e-08]
  Solution norm: 5.367441e-06

As we have computed the magnetic potential, we can now calculate the magnetic field by setting \(\mathbf{B} = \nabla \times A_z\). Note that, since we have chosen a function space of first-order piecewise linear functions to represent the potential, the curl of a function in this space is a discontinuous zeroth-order function (i.e., a function that is constant on each cell). We use dolfinx.fem.Expression to interpolate the curl into the function space W

"""
Magnetic flux density calculation from magnetic vector potential.
This code computes B = ∇ × A where A = A_z ẑ in 2D.
Result: B = (∂A_z/∂y, -∂A_z/∂x) = (B_x, B_y)
"""

def calculate_magnetic_field(mesh, A_z):
    """
    Magnetic field calculation
    
    Parameters:
    -----------
    mesh : dolfinx.mesh.Mesh
        Computational mesh
    A_z : dolfinx.fem.Function
        Magnetic vector potential (z-component)
        
    Returns:
    --------
    B : dolfinx.fem.Function
        Magnetic flux density vector field (B_x, B_y)
    """
    
    print("Calculating magnetic flux density B = ∇ × A...")
    
    # Create vector function space for B field
    # DG(0) = piecewise constant discontinuous elements
    # (mesh.geometry.dim, ) creates vector space with 2 components in 2D
    W = functionspace(mesh, ("DG", 0, (mesh.geometry.dim, )))
    
    # Create function to store magnetic flux density
    B = Function(W)
    B.name = "MagneticFluxDensity"
    
    # Calculate B = ∇ × A = (∂A_z/∂y, -∂A_z/∂x) in 2D
    # A_z.dx(0) = ∂A_z/∂x (derivative w.r.t. first coordinate)  
    # A_z.dx(1) = ∂A_z/∂y (derivative w.r.t. second coordinate)
    B_expr = Expression(
        as_vector((A_z.dx(1), -A_z.dx(0))), 
        W.element.interpolation_points()
    )
    
    # Interpolate the expression onto the DG function space
    B.interpolate(B_expr)
    
    # Calculate magnitude for reporting
    B_magnitude = np.sqrt(B.x.array[0::2]**2 + B.x.array[1::2]**2)
    
    print("✅ Magnetic flux density calculated successfully!")
    print(f"  B_x range: [{B.x.array[0::2].min():.6e}, {B.x.array[0::2].max():.6e}] T")
    print(f"  B_y range: [{B.x.array[1::2].min():.6e}, {B.x.array[1::2].max():.6e}] T") 
    print(f"  |B| range: [{B_magnitude.min():.6e}, {B_magnitude.max():.6e}] T")
    
    return B

B = calculate_magnetic_field(mesh, A_z)
Calculating magnetic flux density B = ∇ × A...
✅ Magnetic flux density calculated successfully!
  B_x range: [-3.938131e-07, 3.939002e-07] T
  B_y range: [-3.950563e-07, 3.951606e-07] T
  |B| range: [2.760445e-15, 3.951684e-07] T

Note that we use ufl.as_vector to interpret the Python tuple (A_z.dx(1), -A_z.dx(0)) as a vector in UFL

We now plot the magnetic potential A_z and the magnetic field B. To do this, we first create a new plotter

plotter = pyvista.Plotter(off_screen=False)

Az_grid = pyvista.UnstructuredGrid(*vtk_mesh(V))
Az_grid.point_data["A_z"] = A_z.x.array
Az_grid.set_active_scalars("A_z")

warp = Az_grid.warp_by_scalar("A_z", factor=1e7)
actor = plotter.add_mesh(warp, show_edges=True)

if not pyvista.OFF_SCREEN:
    #plotter.show()
    plotter.export_html(results_folder/"Az.html")    
else:
    Az_fig = plotter.screenshot(results_folder/"Az.png")

Visualizing the magnetic field

Since the magnetic field is a piecewise-constant vector field, we need to create a custom plotting function. We begin by computing the midpoints of each cell, which are the locations where we want to visualize the cell-wise constant vectors. Next, we extract the data from the function B and reshape it into 3D vectors. Finally, we associate each vector with its corresponding midpoint using pyvista.PolyData

"""
Magnetic field visualization using PyVista for 2D electromagnetic simulation.
This code creates vector glyphs to visualize the magnetic flux density B field.
"""

def visualize_magnetic_field(mesh, B, scale_factor=2e6):
    """
    Magnetic field visualization
    
    Parameters:
    -----------
    mesh : dolfinx.mesh.Mesh
        The computational mesh
    B : dolfinx.fem.Function
        Magnetic flux density vector field
    scale_factor : float
        Scaling factor for vector glyphs
        
    Returns:
    --------
    plotter : pyvista.Plotter
        Configured plotter object
    """
    
    print("Setting up magnetic field visualization...")
    
    # Extract function space information from B
    W = B.function_space  # Get function space from B field

    # Create plotter
    plotter = pyvista.Plotter(off_screen=False)
    plotter.set_position([0, 0, 5])  # Camera position
    
    # -----------------------------------------------------------------------
    # MESH SETUP (with ghost cells for parallel processing)
    # -----------------------------------------------------------------------
    
    # Get topology information including ghost cells
    top_imap = mesh.topology.index_map(mesh.topology.dim)
    num_cells = top_imap.size_local + top_imap.num_ghosts
    
    print(f"Total cells (including ghosts): {num_cells}")
    
    # Ensure connectivity is created
    mesh.topology.create_connectivity(mesh.topology.dim, mesh.topology.dim)
    
    # Compute cell midpoints for vector placement
    cell_indices = np.arange(num_cells, dtype=np.int32)
    midpoints = compute_midpoints(mesh, mesh.topology.dim, cell_indices)
    
    # -----------------------------------------------------------------------
    # VECTOR FIELD DATA PREPARATION
    # -----------------------------------------------------------------------
    
    # Get DOF information 
    num_dofs = W.dofmap.index_map.size_local + W.dofmap.index_map.num_ghosts
    block_size = W.dofmap.index_map_bs  # Should be 2 for 2D vector field
    
    print(f"DOFs: {num_dofs}, Block size: {block_size}")
    
    # Verify consistency
    assert num_cells == num_dofs, f"Mismatch: {num_cells} cells vs {num_dofs} DOFs"
    
    # Prepare 3D vector data (PyVista requires 3D vectors)
    values = np.zeros((num_dofs, 3), dtype=np.float64)
    
    # Reshape B field data and assign to first 2 components
    # B.x.array is [Bx0, By0, Bx1, By1, ...] for DG elements
    B_reshaped = B.x.array.real.reshape(num_dofs, block_size)
    values[:, :mesh.geometry.dim] = B_reshaped  # Fill (Bx, By, 0)
    
    print(f"B field range: [{np.linalg.norm(values, axis=1).min():.3e}, "
          f"{np.linalg.norm(values, axis=1).max():.3e}] T")
    
    # -----------------------------------------------------------------------
    # PYVISTA VISUALIZATION SETUP  
    # -----------------------------------------------------------------------
    
    # Create point cloud at cell midpoints
    cloud = pyvista.PolyData(midpoints)
    cloud["B"] = values  # Attach vector field data
    
    # Create vector glyphs (arrows) 
    glyphs = cloud.glyph("B", factor=scale_factor)
    
    # Add wireframe mesh
    try:
        # Convert DOLFINx mesh to PyVista grid
        grid = vtk_mesh(mesh, mesh.topology.dim)[0]
        actor_mesh = plotter.add_mesh(grid, style="wireframe", color="k", 
                                     line_width=1, opacity=0.3)
    except Exception as e:
        print(f"⚠️  Could not add mesh wireframe: {e}")
        actor_mesh = None
    
    # Add vector field glyphs
    actor_vectors = plotter.add_mesh(glyphs, color="red", 
                                   scalar_bar_args={"title": "B [T]"})
    
    # Set up camera and view
    plotter.camera_position = "xy"  # Top-down view for 2D
    plotter.add_axes()
    plotter.show_grid()
    
    print("✅ Visualization setup complete!")
    
    return plotter

plotter = visualize_magnetic_field(mesh, B)
Setting up magnetic field visualization...
Total cells (including ghosts): 21689
DOFs: 21689, Block size: 2
B field range: [2.760e-15, 3.952e-07] T
⚠️  Could not add mesh wireframe: NumPy array could not be wrapped pyvista.
✅ Visualization setup complete!
if not pyvista.OFF_SCREEN:
    #plotter.show()
    plotter.export_html(results_folder/"B.html")    
else:
    Az_fig = plotter.screenshot(results_folder/"B.png")

K.9 Best Practices for FEniCSx

K.9.1 Solver configuration

Author: Jørgen S. Dokken

In this section, we demonstrate how to specify the linear algebra solver to be used for solving our PDEs, and how to verify the implementation by examining convergence rates:

\[-\Delta u = f \quad \text{in } \Omega, \qquad u = u_D \quad \text{on } \partial \Omega\]

Using the manufactured solution \(u_D = \cos(2\pi x)\cos(2\pi y)\), we obtain the right-hand side function \(f = 8\pi^2 \cos(2\pi x)\cos(2\pi y)\)

We begin by creating a generic module that evaluates the analytical solution at any point \(x\)

import numpy
from mpi4py import MPI
from petsc4py import PETSc

from dolfinx.mesh import create_unit_square, locate_entities_boundary
from dolfinx.fem import dirichletbc, functionspace, Function, locate_dofs_topological
from dolfinx.fem.petsc import LinearProblem

import ufl
from ufl import SpatialCoordinate, TestFunction, TrialFunction, div, dx, inner, grad


def u_ex(mod):
    return lambda x: mod.cos(2 * mod.pi * x[0]) * mod.cos(2 * mod.pi * x[1])

Note that the return type of u_ex is a lambda function. Therefore, we can define two separate lambda functions: one using NumPy (for interpolation) and one using UFL (for defining the source term)

u_numpy = u_ex(numpy)
u_ufl = u_ex(ufl)

We begin by defining the source term in UFL, using ufl.SpatialCoordinate as the input to u_ufl

mesh = create_unit_square(MPI.COMM_WORLD, 30, 30)
x = SpatialCoordinate(mesh)
f = -div(grad(u_ufl(x)))

Next, let us define our linear variational problem

V = functionspace(mesh, ("Lagrange", 1))
u = TrialFunction(V)
v = TestFunction(V)

a = inner(grad(u), grad(v)) *dx
L = f *v *dx

u_bc = Function(V)
u_bc.interpolate(u_numpy)

facets = locate_entities_boundary(
  mesh, 
  mesh.topology.dim -1, 
  lambda x: numpy.full(x.shape[1], True)
)
dofs = locate_dofs_topological(V, mesh.topology.dim -1, facets)
bcs = [dirichletbc(u_bc, dofs)]

We begin by solving the problem using LU factorization, a direct solver method similar to Gaussian elimination

default_problem = LinearProblem(
  a, 
  L, 
  bcs=bcs,
  petsc_options={"ksp_type": "preonly", "pc_type": "lu"}
)
uh = default_problem.solve()

We now examine the solver process by inspecting the PETSc solver. Since the view options in PETSc are not adapted for notebooks (for example, solver.view() prints output to the terminal when used in a .py file), we instead write the solver output to a file, read it back, and then print it

from pathlib import Path

results_folder = Path("fenicsx/best_practices")
results_folder.mkdir(exist_ok=True, parents=True)

lu_solver = default_problem.solver
viewer = PETSc.Viewer().createASCII(str(results_folder/"lu_output.txt"))
lu_solver.view(viewer)
viewer.destroy()

with open(str(results_folder/"lu_output.txt"), "r") as solver_output:
  for line in solver_output:
      print(line.rstrip()) 
KSP Object: (dolfinx_solve_15334798544) 1 MPI process
  type: preonly
  maximum iterations=10000, initial guess is zero
  tolerances: relative=1e-05, absolute=1e-50, divergence=10000.
  left preconditioning
  using NONE norm type for convergence test
PC Object: (dolfinx_solve_15334798544) 1 MPI process
  type: lu
    out-of-place factorization
    tolerance for zero pivot 2.22045e-14
    matrix ordering: nd
    factor fill ratio given 5., needed 5.08301
      Factored matrix follows:
        Mat Object: (dolfinx_solve_15334798544) 1 MPI process
          type: seqaij
          rows=961, cols=961
          package used to perform factorization: petsc
          total: nonzeros=32943, allocated nonzeros=32943
            not using I-node routines
  linear system matrix = precond matrix:
  Mat Object: (dolfinx_solve_15334798544) 1 MPI process
    type: seqaij
    rows=961, cols=961
    total: nonzeros=6481, allocated nonzeros=6481
    total number of mallocs used during MatSetValues calls=0
      not using I-node routines

This is a robust and straightforward method, and it is recommended for problems with up to a few thousand unknowns. It can be used efficiently for many 2D problems and smaller 3D problems. However, sparse LU decomposition quickly becomes inefficient, since for an \(N \times N\) matrix the number of floating-point operations scales as \(\sim \tfrac{2}{3}N^3\)

For larger problems, we instead turn to iterative methods, which are faster and require less memory

How to choose a linear solver and preconditioner

Since the Poisson equation leads to a symmetric, positive-definite system matrix, the optimal Krylov solver is the conjugate gradient (CG) method. By default, the preconditioner is incomplete LU factorization (ILU), a widely used and robust choice

The preconditioner can be changed by setting “pc_type” to any of the other PETSc preconditioners, as listed in the PETSc KSP solvers and PETSc preconditioners documentation

Any PETSc option can be set through the petsc_options input, including the absolute tolerance (“ksp_atol”), relative tolerance (“ksp_rtol”), and maximum number of iterations (“ksp_max_it”)

cg_problem = LinearProblem(
  a, 
  L, 
  bcs=bcs,
  petsc_options={
    "ksp_type": "cg", 
    "ksp_rtol": 1e-6, 
    "ksp_atol": 1e-10, 
    "ksp_max_it": 1000
  }
)
uh = cg_problem.solve()

cg_solver = cg_problem.solver
viewer = PETSc.Viewer().createASCII(str(results_folder/"cg_output.txt"))
cg_solver.view(viewer)
viewer.destroy()

with open(str(results_folder/"cg_output.txt"), "r") as solver_output:
  for line in solver_output.readlines():
      print(line.rstrip())    
KSP Object: (dolfinx_solve_15334860416) 1 MPI process
  type: cg
  maximum iterations=1000, initial guess is zero
  tolerances: relative=1e-06, absolute=1e-10, divergence=10000.
  left preconditioning
  using PRECONDITIONED norm type for convergence test
PC Object: (dolfinx_solve_15334860416) 1 MPI process
  type: ilu
    out-of-place factorization
    0 levels of fill
    tolerance for zero pivot 2.22045e-14
    matrix ordering: natural
    factor fill ratio given 1., needed 1.
      Factored matrix follows:
        Mat Object: (dolfinx_solve_15334860416) 1 MPI process
          type: seqaij
          rows=961, cols=961
          package used to perform factorization: petsc
          total: nonzeros=6481, allocated nonzeros=6481
            not using I-node routines
  linear system matrix = precond matrix:
  Mat Object: (dolfinx_solve_15334860416) 1 MPI process
    type: seqaij
    rows=961, cols=961
    total: nonzeros=6481, allocated nonzeros=6481
    total number of mallocs used during MatSetValues calls=0
      not using I-node routines

For non-symmetric systems, it is preferable to use a Krylov solver designed for such problems, for example GMRES

gmres_problem = LinearProblem(
  a, 
  L, 
  bcs=bcs,
  petsc_options={
    "ksp_type": "gmres", 
    "ksp_rtol": 1e-6, 
    "ksp_atol": 1e-10, 
    "ksp_max_it": 1000, 
    "pc_type": "none"
  }
)
uh = gmres_problem.solve()

gmres_solver = gmres_problem.solver
viewer = PETSc.Viewer().createASCII(str(results_folder/"gmres_output.txt"))
gmres_solver.view(viewer)
viewer.destroy()

with open(str(results_folder/"gmres_output.txt"), "r") as solver_output:
  for line in solver_output.readlines():
      print(line.rstrip())       
KSP Object: (dolfinx_solve_15344590032) 1 MPI process
  type: gmres
    restart=30, using Classical (unmodified) Gram-Schmidt Orthogonalization with no iterative refinement
    happy breakdown tolerance 1e-30
  maximum iterations=1000, initial guess is zero
  tolerances: relative=1e-06, absolute=1e-10, divergence=10000.
  left preconditioning
  using PRECONDITIONED norm type for convergence test
PC Object: (dolfinx_solve_15344590032) 1 MPI process
  type: none
  linear system matrix = precond matrix:
  Mat Object: (dolfinx_solve_15344590032) 1 MPI process
    type: seqaij
    rows=961, cols=961
    total: nonzeros=6481, allocated nonzeros=6481
    total number of mallocs used during MatSetValues calls=0
      not using I-node routines
Note

When using manufactured solutions, we often expect the error to be close to machine precision. However, this becomes more complicated when iterative methods are employed. The key issue is ensuring that the error introduced by the iterative solver remains smaller than the tolerance used in the convergence test. For linear elements and small meshes, a tolerance in the range of \(10^{-12}\) to \(10^{-14}\) also works well when using Krylov solvers

K.9.2 JIT options and visualization using Pandas

Author: Jørgen S. Dokken

In this section, we explore how to optimize and inspect the integration kernels used in dolfinx. As seen in the previous demos, dolfinx uses the Unified Form Language (UFL) to describe variational problems

These UFL descriptions must be translated into code for assembling the right- and left-hand sides of the discrete variational problem

dolfinx uses ffcx to generate efficient C code for assembling element matrices. This C code is then compiled via CFFI, and a variety of compilation options can be specified

We begin by specifying the current directory as the location to store the generated C files. The current directory is obtained using pathlib

import time
from typing import Dict
from pathlib import Path

from mpi4py import MPI
import pandas as pd

import matplotlib.pyplot as plt
import seaborn

from dolfinx.mesh import create_unit_cube
from dolfinx.fem import functionspace, form
from dolfinx.fem.petsc import assemble_matrix

import ufl
from ufl import TestFunction, TrialFunction, dx, inner

cache_dir = f"{str(Path.cwd())}/.cache"
print(f"Directory to put C files in: {cache_dir}")
Directory to put C files in: /Users/kyyoo/Documents/notebooks/SeoulTechPSE.github.io/.cache

Next, we generate a general function to assemble the mass matrix for a unit cube. Note that we use dolfinx.fem.form to compile the variational form. For code that uses dolfinx.fem.petsc.LinearProblem, you can pass jit_options as a keyword argument

def compile_form(space: str, degree: int, jit_options: Dict):
    N = 10
    mesh = create_unit_cube(MPI.COMM_WORLD, N, N, N)
    
    V = functionspace(mesh, (space, degree))
    u = TrialFunction(V)
    v = TestFunction(V)
    
    a = inner(u, v) *dx
    a_compiled = form(a, jit_options=jit_options)
    
    start = time.perf_counter()
    assemble_matrix(a_compiled)
    end = time.perf_counter()
    
    return end -start

We begin by examining the different levels of optimization that the C compiler can apply to the generated code. A list of available optimization options, along with their explanations, can be found here

optimization_options = ["-O1", "-O2", "-O3", "-Ofast"]

The next option to consider is whether to compile the code with -march=native. This option enables CPU-specific instructions for the local machine, which can lead to different results on different systems. More information can be found here

march_native = [True, False]

We select a subset of finite element spaces and vary the order of each space to examine how it affects the assembly time under different compilation option

results = {"Space": [], "Degree": [], "Options": [], "Time": []}
for space in ["N1curl", "Lagrange", "RT"]:
  for degree in [1, 2, 3]:
    for native in march_native:
      for option in optimization_options:
        if native:
          cffi_options = [option, "-march=native"]
        else:
          cffi_options = [option]
        jit_options = {
          "cffi_extra_compile_args": cffi_options,
          "cache_dir": cache_dir, 
          "cffi_libraries": ["m"]
        }
        
        runtime = compile_form(space, degree, jit_options=jit_options)

        results["Space"].append(space)
        results["Degree"].append(str(degree))
        results["Options"].append("\n".join(cffi_options))
        results["Time"].append(runtime)

We have now stored all the results in a dictionary. To visualize them, we use pandas and its DataFrame class. In a Jupyter notebook, the data can be inspected as follows:

results_df = pd.DataFrame.from_dict(results)
results_df
Space Degree Options Time
0 N1curl 1 -O1\n-march=native 0.015093
1 N1curl 1 -O2\n-march=native 0.015046
2 N1curl 1 -O3\n-march=native 0.014177
3 N1curl 1 -Ofast\n-march=native 0.014920
4 N1curl 1 -O1 0.015742
... ... ... ... ...
67 RT 3 -Ofast\n-march=native 0.454098
68 RT 3 -O1 0.475202
69 RT 3 -O2 0.458539
70 RT 3 -O3 0.453172
71 RT 3 -Ofast 0.459930

72 rows × 4 columns

We can now create a plot for each element type to visualize how the results vary with different compilation options. A new column is created for each element type and degree

seaborn.set(style="ticks")
seaborn.set_style("darkgrid")

results_df["Element"] = results_df["Space"] +" " +results_df["Degree"]
hue_order = sorted(results_df["Space"].unique())
for degree in [1, 2, 3]:
  df_degree = results_df[results_df["Degree"] == str(degree)]

  g = seaborn.catplot(
    x="Options", 
    y="Time", 
    hue="Space",
    hue_order=hue_order, 
    kind="bar", 
    data=df_degree,
    height=3,
    aspect=4.0)
  g.fig.suptitle(f"Degree = {degree}", y=1.02)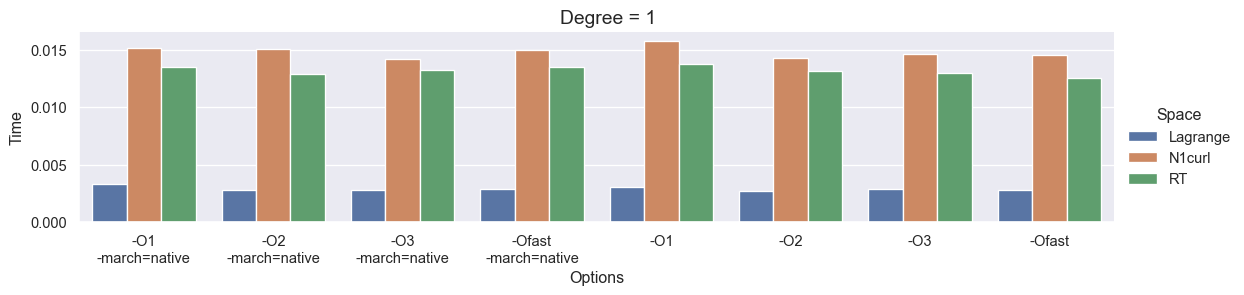

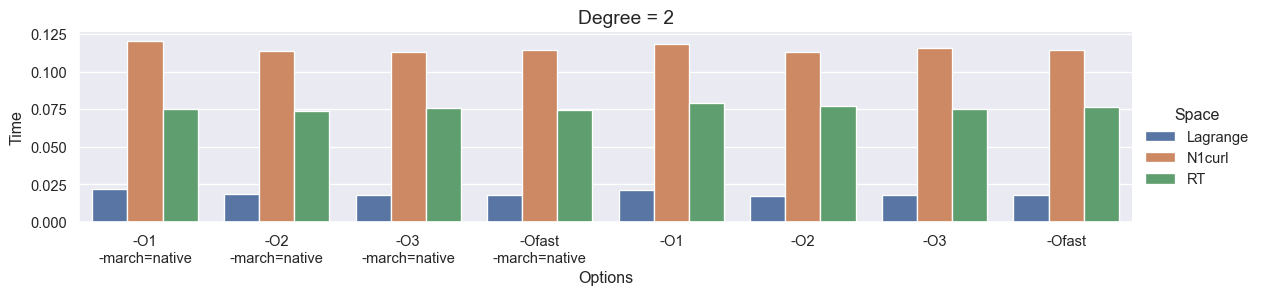
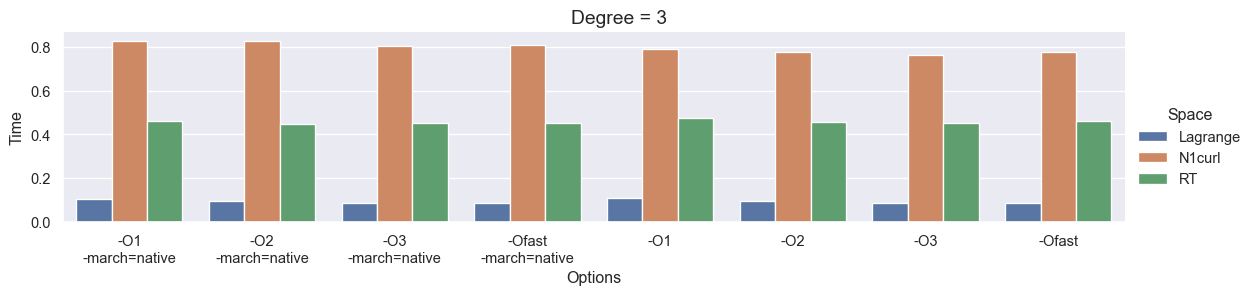
We observe that the compile time increases as the degree of the function space grows, and that the greatest speedup is achieved when using -O3 or -Ofast in combination with -march=native

K.9.3 Error control: Computing convergence rates

Author: Jørgen S. Dokken, Hans Petter Langtangen, Anders Logg

For any numerical method, one of the most fundamental questions is its convergence rate: how fast the error decreases as the resolution is increased (i.e., as the mesh size is decreased)

In the finite element method, this typically involves proving—either theoretically or empirically—that the error \(\| u - u_h \|\) is bounded by a constant times the mesh size \(h\) raised to some power \(p\), that is,

\[\| u - u_h \| \le C \, h^p\]

for some constant \(C\) independent of the mesh. The number \(p\) is called the convergence rate of the method. Note that different norms, such as the \(L^2\)-norm or the \(H^1\)-norm, generally yield different convergence rates

Computing error norms

We first construct a manufactured problem based on the same configuration used in the solver

import numpy as np
from mpi4py import MPI

from dolfinx import default_scalar_type
from dolfinx.mesh import create_unit_square, locate_entities_boundary
from dolfinx.fem import (Expression, Function, functionspace,
                         assemble_scalar, dirichletbc, form, locate_dofs_topological)
from dolfinx.fem.petsc import LinearProblem

import ufl
from ufl import (SpatialCoordinate, TestFunction, TrialFunction, 
                 div, dot, dx, grad, inner)

def u_ex(mod):
  return lambda x: mod.cos(2 *mod.pi *x[0]) *mod.cos(2 *mod.pi *x[1])

u_numpy = u_ex(np)
u_ufl = u_ex(ufl)

def solve_poisson(N=10, degree=1):

  mesh = create_unit_square(MPI.COMM_WORLD, N, N)
    
  x = SpatialCoordinate(mesh)
  f = -div(grad(u_ufl(x)))
    
  V = functionspace(mesh, ("Lagrange", degree))
  u = TrialFunction(V)
  v = TestFunction(V)
    
  a = inner(grad(u), grad(v)) *dx
  L = f *v *dx
    
  u_bc = Function(V)
  u_bc.interpolate(u_numpy)
    
  facets = locate_entities_boundary(
    mesh, 
    mesh.topology.dim -1, 
    lambda x: np.full(x.shape[1], True)
  )
  dofs = locate_dofs_topological(
    V, 
    mesh.topology.dim -1, 
    facets
  )
  bcs = [dirichletbc(u_bc, dofs)]
    
  default_problem = LinearProblem(
    a, 
    L, 
    bcs=bcs, 
    petsc_options={"ksp_type": "preonly", "pc_type": "lu"}
  )

  return default_problem.solve(), u_ufl(x)

Now, we compute the error between the analytical solution \(u_{\text{ex}} = u_{\text{ufl}}(x)\) and the approximate solution \(u_h\). The \(L^2\)-norm of the error

\[\| u_e - u_h \|_{L^2(\Omega)} = \left( \int_\Omega |u_e - u_h|^2 \, dx \right)^{1/2}\]

measures the pointwise accuracy of the approximate solution in an average sense. It quantifies how close \(u_h\) is to \(u_e\) in terms of their values

uh, u_ex = solve_poisson(10)
comm = uh.function_space.mesh.comm

error_L2 = form((uh -u_ex)**2 *ufl.dx)
E_L2 = np.sqrt(comm.allreduce(assemble_scalar(error_L2), MPI.SUM))

if comm.rank == 0:
  print(f"L2-error: {E_L2:.2e}")
L2-error: 5.28e-02

Sometimes it is of interest to compute the error of the gradient field, \(\| \nabla (u_e - u_h) \|\), often referred to as the \(H_0^1\)-norm of the error. This can be expressed as

\[\left( \int_\Omega \lvert \nabla (u_e - u_h) \rvert^2 \, dx \right)^{1/2}\]

The \(H_0^1\)-norm measures the error in the so-called energy space, which is particularly relevant for elliptic partial differential equations, as it reflects how well the numerical solution captures the energy of the exact solution

eh = uh -u_ex
error_H10 = form(dot(grad(eh), grad(eh)) *dx)
E_H10 = np.sqrt(comm.allreduce(assemble_scalar(error_H10), op=MPI.SUM))

if comm.rank == 0:
  print(f"H01-error: {E_H10:.2e}")
H01-error: 1.36e+00

Reliable error norm computation

However, expanding the expression gives

\[(u_{\text{ex}} - u_h)^2 = u_{\text{ex}}^2 + u_h^2 - 2u_{\text{ex}}u_h\]

If the error is small (while the solutions themselves are of moderate size), this calculation involves subtracting two quantities of order one—namely \(u_{\text{ex}}^2 + u_h^2 \sim 1\) and \(2u_{\text{ex}}u_h \sim 1\)—to obtain a much smaller number. This subtraction is prone to round-off errors

To avoid this issue, we interpolate both the approximate and the exact solutions into a higher-order function space. We then subtract their degrees of freedom to form an explicit error function. Finally, we assemble (integrate) the squared error and take the square root to obtain the \(L^2\)-norm

def error_L2(uh, u_ex, degree_raise=3):

  # Create higher order function space
  mesh = uh.function_space.mesh
  degree = uh.function_space.ufl_element().degree
  family = uh.function_space.ufl_element().family_name
    
  W = functionspace(mesh, (family, degree +degree_raise))
    
  # Interpolate approximate solution
  u_W = Function(W)
  u_W.interpolate(uh)

  # Interpolate exact solution, special handling if exact solution
  # is a ufl expression or a python lambda function
  u_ex_W = Function(W)
  if isinstance(u_ex, ufl.core.expr.Expr):
    u_expr = Expression(u_ex, W.element.interpolation_points())
    u_ex_W.interpolate(u_expr)
  else:
    u_ex_W.interpolate(u_ex)

  # Compute the error in the higher order function space
  e_W = Function(W)
  e_W.x.array[:] = u_W.x.array -u_ex_W.x.array

  # Integrate the error
  error = form(ufl.inner(e_W, e_W) *ufl.dx)
  error_local = assemble_scalar(error)
  error_global = mesh.comm.allreduce(error_local, op=MPI.SUM)
  
  return np.sqrt(error_global)

Computing convergence rates

Let us consider a sequence of mesh resolutions

\[h_0 > h_1 > h_2 > \cdots, \qquad h_i = \frac{1}{N_i}\]

where \(N_i\) denotes the number of subdivisions (or degrees of freedom) in the discretization. We compute the numerical error for a range of values of \(N_i\)

Ns = [4, 8, 16, 32, 64]
Es = np.zeros(len(Ns), dtype=default_scalar_type)
hs = np.zeros(len(Ns), dtype=np.float64)

for i, N in enumerate(Ns):
  uh, u_ex = solve_poisson(N, degree=1)
  comm = uh.function_space.mesh.comm

  # Accepts either u_numpy or u_ex
  # Use u_numpy for L2 error (no JIT needed)
  hs[i] = 1. /Ns[i]
  Es[i] = error_L2(uh, u_numpy)
  if comm.rank == 0:
    print(f"h: {hs[i]:.2e} Error: {Es[i]:.2e}")
h: 2.50e-01 Error: 2.43e-01
h: 1.25e-01 Error: 7.96e-02
h: 6.25e-02 Error: 2.15e-02
h: 3.12e-02 Error: 5.47e-03
h: 1.56e-02 Error: 1.37e-03

If we assume that the error \(E_i\) can be expressed as

\(E_i = C h_i^r\)

with unknown constants \(C\) and \(r\), then by comparing two consecutive experiments

\[E_{i-1} = C h_{i-1}^r, \qquad E_i = C h_i^r\]

we can solve for \(r\):

\[r = \frac{\ln(E_i / E_{i-1})}{\ln(h_i / h_{i-1})}\]

As \(i\) increases, the computed values of \(r\) should approach the expected convergence rate, which in the case of the \(L^2\)-error is typically the polynomial degree plus one. This calculation can be implemented compactly using NumPy

rates = np.log(Es[1:] /Es[:-1]) /np.log(hs[1:] /hs[:-1])
if comm.rank == 0:
  print(f"Rates: {rates}")
Rates: [1.61228695 1.89147568 1.97191247 1.99290382]

We perform a similar study for different polynomial orders to verify the previous claim

degrees = [1, 2, 3, 4]
for degree in degrees:
  hs = np.zeros(len(Ns), dtype=np.float64)
  Es = np.zeros(len(Ns), dtype=default_scalar_type)
    
  for i, N in enumerate(Ns):
    uh, u_ex = solve_poisson(N, degree=degree)
    comm = uh.function_space.mesh.comm

    hs[i] = 1. /Ns[i]    
    Es[i] = error_L2(uh, u_numpy, degree_raise=3)

    if comm.rank == 0:
      print(f"h: {hs[i]:.2e} Error: {Es[i]:.2e}")
    
  rates = np.log(Es[1:] /Es[:-1]) /np.log(hs[1:] /hs[:-1])
  if comm.rank == 0:
    print(f"Polynomial degree {degree:d}, Rates {rates}\n")
h: 2.50e-01 Error: 2.43e-01
h: 1.25e-01 Error: 7.96e-02
h: 6.25e-02 Error: 2.15e-02
h: 3.12e-02 Error: 5.47e-03
h: 1.56e-02 Error: 1.37e-03
Polynomial degree 1, Rates [1.61228695 1.89147568 1.97191247 1.99290382]

h: 2.50e-01 Error: 3.52e-02
h: 1.25e-01 Error: 4.39e-03
h: 6.25e-02 Error: 5.50e-04
h: 3.12e-02 Error: 6.88e-05
h: 1.56e-02 Error: 8.60e-06
Polynomial degree 2, Rates [3.00109101 2.99828073 2.99822291 2.99930786]

h: 2.50e-01 Error: 5.54e-03
h: 1.25e-01 Error: 3.35e-04
h: 6.25e-02 Error: 1.99e-05
h: 3.12e-02 Error: 1.21e-06
h: 1.56e-02 Error: 7.49e-08
Polynomial degree 3, Rates [4.04795047 4.07357659 4.03728992 4.01645269]

h: 2.50e-01 Error: 7.20e-04
h: 1.25e-01 Error: 2.42e-05
h: 6.25e-02 Error: 7.75e-07
h: 3.12e-02 Error: 2.44e-08
h: 1.56e-02 Error: 7.64e-10
Polynomial degree 4, Rates [4.896908   4.96084158 4.98926012 4.99766448]

Infinity norm estimates

We first define a function to evaluate the infinity norm, i.e., the maximum pointwise error between the numerical and exact solutions

def error_infinity(u_h, u_ex):
  # Interpolate exact solution (UFL or lambda handled separately)
  u_ex_V = Function(u_h.function_space)
  comm = u_h.function_space.mesh.comm
    
  if isinstance(u_ex, ufl.core.expr.Expr):
    u_expr = Expression(u_ex, u_h.function_space.element.interpolation_points())
    u_ex_V.interpolate(u_expr)
  else:
    u_ex_V.interpolate(u_ex)

  # Compute global infinity norm from local maxima  
  error_max_local = np.max(np.abs(u_h.x.array -u_ex_V.x.array))
  error_max = comm.allreduce(error_max_local, op=MPI.MAX)

  return error_max

Performing this procedure for various polynomial degrees produces the following results:

for degree in degrees:
  hs = np.zeros(len(Ns), dtype=np.float64)    
  Es = np.zeros(len(Ns), dtype=default_scalar_type)

  for i, N in enumerate(Ns):
    uh, u_ex = solve_poisson(N, degree=degree)
    comm = uh.function_space.mesh.comm

    hs[i] = 1. /Ns[i]    
    Es[i] = error_infinity(uh, u_numpy)

    if comm.rank == 0:
       print(f"h: {hs[i]:.2e} Error: {Es[i]:.2e}")
    
  rates = np.log(Es[1:] /Es[:-1]) /np.log(hs[1:] /hs[:-1])
  if comm.rank == 0:
    print(f"Polynomial degree {degree:d}, Rates {rates}\n")
h: 2.50e-01 Error: 2.73e-01
h: 1.25e-01 Error: 6.96e-02
h: 6.25e-02 Error: 1.75e-02
h: 3.12e-02 Error: 4.38e-03
h: 1.56e-02 Error: 1.10e-03
Polynomial degree 1, Rates [1.96828918 1.9917697  1.99791282 1.99947611]

h: 2.50e-01 Error: 4.85e-02
h: 1.25e-01 Error: 3.65e-03
h: 6.25e-02 Error: 2.37e-04
h: 3.12e-02 Error: 1.50e-05
h: 1.56e-02 Error: 9.38e-07
Polynomial degree 2, Rates [3.73213705 3.94227924 3.98612529 3.99656575]

h: 2.50e-01 Error: 1.08e-02
h: 1.25e-01 Error: 8.13e-04
h: 6.25e-02 Error: 5.86e-05
h: 3.12e-02 Error: 3.80e-06
h: 1.56e-02 Error: 2.41e-07
Polynomial degree 3, Rates [3.72903577 3.79406598 3.94800701 3.97888408]

h: 2.50e-01 Error: 1.63e-03
h: 1.25e-01 Error: 5.23e-05
h: 6.25e-02 Error: 1.67e-06
h: 3.12e-02 Error: 5.25e-08
h: 1.56e-02 Error: 1.64e-09
Polynomial degree 4, Rates [4.96133103 4.96807694 4.99161588 4.99787562]

We observe superconvergence for second-order polynomials, resulting in an observed fourth-order convergence

K.9.4 Custom Newton solvers

Author: Jørgen S. Dokken

Newton’s Method, as used in the non-linear Poisson problem, is a technique for solving a non-linear equation by iteratively solving a sequence of linear equations. Given a function \(F:\mathbb{R}^M \to \mathbb{R}^M\), the iterates \(u_k, u_{k+1} \in \mathbb{R}^M\) satisfy

\[u_{k+1} = u_k - J_F(u_k)^{-1} F(u_k)\]

where \(J_F(u_k)\) is the Jacobian matrix of \(F\) at \(u_k\)

Introducing the increment \(\delta u_k = u_{k+1} - u_k\), this can be rewritten as the linear system

\[J_F(u_k) \, \delta u_k = - F(u_k)\]

with the update

\[u_{k+1} = u_k + \delta u_k\]

Problem specification

We start by importing the required libraries

import numpy as np
from mpi4py import MPI
from petsc4py import PETSc

import matplotlib.pyplot as plt
import pyvista

import dolfinx
import dolfinx.fem.petsc

import ufl

plt.style.use('default')

We consider the following non-linear problem:

\[u^2 - 2u = x^2 + 4x + 3 \quad \text{for } x \in [0,1]\]

This problem has two solutions: \(u = -x - 1\) and \(u = x + 3\). We define these roots as Python functions and create an appropriate array of points for plotting the solutions

def root_0(x):
  return 3 +x[0]

def root_1(x):
  return -1 -x[0]

N = 10
x_spacing = np.linspace(0, 1, N)
roots = [root_0, root_1]

Starting with the initial guess \(u_0 = 0\), we then define the mesh, the function space, and the function uh for the numerical solution

mesh = dolfinx.mesh.create_unit_interval(MPI.COMM_WORLD, N)

V = dolfinx.fem.functionspace(mesh, ("Lagrange", 1))
uh = dolfinx.fem.Function(V)

Definition of residual and Jacobian

We then formulate the variational problem by multiplying with a test function and integrating over the domain \([0,1]\)

v = ufl.TestFunction(V)

x = ufl.SpatialCoordinate(mesh)
F = uh**2 *v *ufl.dx -2 *uh *v *ufl.dx -(x[0]**2 +4 *x[0] +3) *v *ufl.dx
residual = dolfinx.fem.form(F)

The Jacobian \(J_F\) is then obtained by applying ufl.derivative to the variational form

J = ufl.derivative(F, uh)
jacobian = dolfinx.fem.form(J)

As the problem will be solved iteratively, the sparse matrix and residual vector are assembled only once

Setup of iteration-independent structures

A = dolfinx.fem.petsc.create_matrix(jacobian)
L = dolfinx.fem.petsc.create_vector(residual)

We then set up the linear solver together with a vector to hold the update du

solver = PETSc.KSP().create(mesh.comm)
solver.setOperators(A)

du = dolfinx.fem.Function(V)

To monitor the evolution of uh during the iterations, we obtain the DoF coordinates and sort them in ascending order

coords = V.tabulate_dof_coordinates()[:, 0]
sort_order = np.argsort(coords)

max_iterations = 25
solutions = np.zeros((max_iterations +1, len(coords)))
solutions[0] = uh.x.array[sort_order]

At this stage, we are ready to solve the linearized problem. For each iteration, the Jacobian and residual are reassembled, and the norm of the update (dx) is used as the stopping criterion

i = 0
while i < max_iterations:
  # Assemble Jacobian and residual
  with L.localForm() as loc_L:
    loc_L.set(0)
  A.zeroEntries()
  dolfinx.fem.petsc.assemble_matrix(A, jacobian)
  A.assemble()
  dolfinx.fem.petsc.assemble_vector(L, residual)
  L.ghostUpdate(addv=PETSc.InsertMode.ADD_VALUES, mode=PETSc.ScatterMode.REVERSE)

  # Scale residual by -1
  L.scale(-1)
  L.ghostUpdate(addv=PETSc.InsertMode.INSERT_VALUES, mode=PETSc.ScatterMode.FORWARD)

  # Solve linear problem
  solver.solve(L, du.x.petsc_vec)
  du.x.scatter_forward()
  
  # Update u_{i+1} = u_i + delta u_i
  uh.x.array[:] += du.x.array
  i += 1

  # Compute norm of update
  correction_norm = du.x.petsc_vec.norm(0)  # L^2 norm
  print(f"Iteration {i}: {correction_norm = :.6e}")
  if correction_norm < 1e-10:
    break
  solutions[i, :] = uh.x.array[sort_order]
Iteration 1: correction_norm = 2.941583e+01
Iteration 2: correction_norm = 1.077679e+01
Iteration 3: correction_norm = 2.048893e+00
Iteration 4: correction_norm = 8.991947e-02
Iteration 5: correction_norm = 2.277570e-04
Iteration 6: correction_norm = 2.211497e-09
Iteration 7: correction_norm = 1.123544e-15

At this point, we compute the residual magnitude to monitor convergence

dolfinx.fem.petsc.assemble_vector(L, residual)
print(f"Final residual = {L.norm(0):.6e}")
Final residual = 4.859835e-16

Visualization of Newton iterations

We now study how the solution evolves and quantify its error with respect to the two exact roots of the problem

# Plot solution for each of the iterations
fig = plt.figure(figsize=(8, 6))

for j, solution in enumerate(solutions[:i]):
  plt.plot(coords[sort_order], solution, label=f"Iteration {j}")

# Plot each of the roots of the problem, 
# and compare the approximate solution with each of them
for j, root in enumerate(roots):
  u_ex = root(x)
  
  L2_error = dolfinx.fem.form(ufl.inner(uh -u_ex, uh -u_ex) *ufl.dx)
  global_L2 = mesh.comm.allreduce(
    dolfinx.fem.assemble_scalar(L2_error), 
    op=MPI.SUM
  )
  print(f"L2-error (root {j}) {np.sqrt(global_L2):.6e}")

  plt.plot(x_spacing, root(x_spacing.reshape(1, -1)), ':o', label=f'root_{j}')

plt.xlabel('x')
plt.ylabel('u')
plt.grid()
plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
L2-error (root 0) 5.033223e+00
L2-error (root 1) 1.110223e-16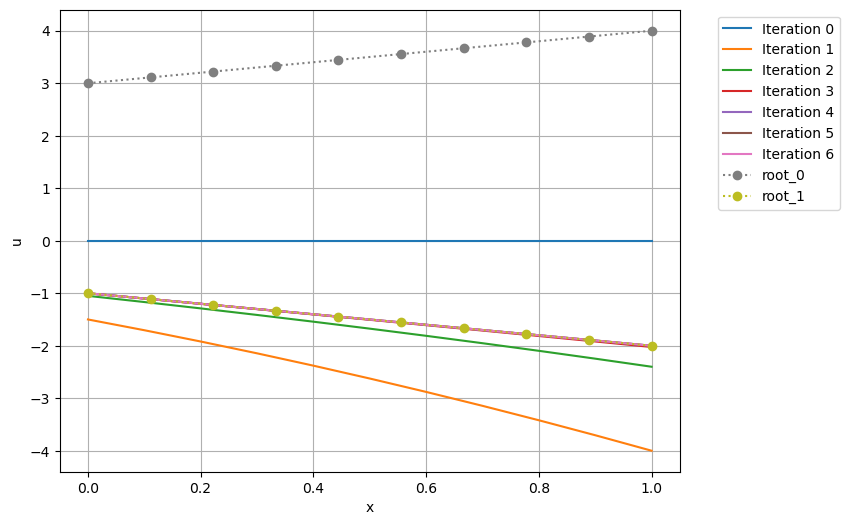

Newton’s method with DirichletBC

In the previous example, we did not incorporate Dirichlet boundary conditions. We now extend the formulation to the non-linear Poisson problem, where such boundary conditions play a central role. As a first step, we define the computational mesh, the analytical solution, and the corresponding forcing term f

def q(u):
  return 1 +u**2

domain = dolfinx.mesh.create_unit_square(MPI.COMM_WORLD, 10, 10)

x = ufl.SpatialCoordinate(domain)
u_ufl = 1 +x[0] +2 *x[1]
f = - ufl.div(q(u_ufl) *ufl.grad(u_ufl))

def u_exact(x):
  return eval(str(u_ufl))

Next, we specify the Dirichlet boundary condition bc, and define the variational residual F together with its Jacobian J

V = dolfinx.fem.functionspace(domain, ("Lagrange", 1))

u_D = dolfinx.fem.Function(V)
u_D.interpolate(u_exact)

fdim = domain.topology.dim -1
domain.topology.create_connectivity(fdim, fdim +1)
boundary_facets = dolfinx.mesh.exterior_facet_indices(domain.topology)
bc = dolfinx.fem.dirichletbc(
  u_D, 
  dolfinx.fem.locate_dofs_topological(V, fdim, boundary_facets)
)

uh = dolfinx.fem.Function(V)
v = ufl.TestFunction(V)

F = q(uh) *ufl.dot(ufl.grad(uh), ufl.grad(v)) *ufl.dx -f *v *ufl.dx
J = ufl.derivative(F, uh)

residual = dolfinx.fem.form(F)
jacobian = dolfinx.fem.form(J)

We then set up the system matrix A, the right-hand side vector L, and the update function du

du = dolfinx.fem.Function(V)

A = dolfinx.fem.petsc.create_matrix(jacobian)
L = dolfinx.fem.petsc.create_vector(residual)

solver = PETSc.KSP().create(mesh.comm)
solver.setOperators(A)

Since this problem has strong Dirichlet boundary conditions, we need to apply a lifting to the right-hand side of our Newton problem. Recall that our goal is to solve the system

\[\begin{aligned} J_F(u_k)\,\delta u_k &= - F(u_k),\\ u_{k+1} &= u_k + \delta u_k \end{aligned}\]

We require that

\[u_{k+1}\vert_{\text{bc}} = u_D\]

However, we do not know if the current iterate satisfies the boundary condition, i.e., whether

\[u_k\vert_{\text{bc}} = u_D\]

To enforce the boundary condition, we therefore apply the following condition on the Newton correction \(\delta u_k\):

\[\delta u_k \vert_{\text{bc}} = u_D - u_k \vert_{\text{bc}}\]

This leads to the following Newton scheme with strong Dirichlet conditions:

\[ \begin{aligned} J_F(u_k)\,\delta u_k &= -F(u_k), & \delta u_k \vert_{\text{bc}} &= u_D - u_k\vert_{\text{bc}},\\ u_{k+1} &= u_k + \delta u_k \end{aligned}\]

i = 0
error = dolfinx.fem.form(
  ufl.inner(uh -u_ufl, uh -u_ufl) *ufl.dx(metadata={"quadrature_degree": 4})
)
L2_error = []
du_norm = []
while i < max_iterations:
  # Assemble Jacobian and residual
  with L.localForm() as loc_L:
    loc_L.set(0)
  A.zeroEntries()
  dolfinx.fem.petsc.assemble_matrix(A, jacobian, bcs=[bc])
  A.assemble()
  dolfinx.fem.petsc.assemble_vector(L, residual)
  L.ghostUpdate(addv=PETSc.InsertMode.ADD, mode=PETSc.ScatterMode.REVERSE)
  L.scale(-1)

  # Compute b - J(u_D-u_(i-1))
  dolfinx.fem.petsc.apply_lifting(
    L, 
    [jacobian], 
    [[bc]], 
    x0=[uh.x.petsc_vec], 
    alpha=1
  )
  
  # Set du|_bc = u_{i-1}-u_D
  dolfinx.fem.petsc.set_bc(L, [bc], uh.x.petsc_vec, 1.0)
  L.ghostUpdate(addv=PETSc.InsertMode.INSERT_VALUES, mode=PETSc.ScatterMode.FORWARD)

  # Solve linear problem
  solver.solve(L, du.x.petsc_vec)
  du.x.scatter_forward()

  # Update u_{i+1} = u_i + delta u_i
  uh.x.array[:] += du.x.array
  i += 1

  # Compute norm of update
  correction_norm = du.x.petsc_vec.norm(0)

  # Compute L2 error comparing to the analytical solution
  L2_error.append(np.sqrt(mesh.comm.allreduce(dolfinx.fem.assemble_scalar(error), op=MPI.SUM)))
  du_norm.append(correction_norm)

  print(f"Iteration {i}: {correction_norm = :.6e}, L2_error = {L2_error[-1]:.6e}")
  if correction_norm < 1e-10:
    break
Iteration 1: correction_norm = 2.174258e+02, L2_error = 1.009449e+00
Iteration 2: correction_norm = 1.546085e+02, L2_error = 1.025886e+00
Iteration 3: correction_norm = 4.927247e+01, L2_error = 3.541886e-01
Iteration 4: correction_norm = 1.695612e+01, L2_error = 7.129374e-02
Iteration 5: correction_norm = 3.166798e+00, L2_error = 4.565047e-03
Iteration 6: correction_norm = 1.713648e-01, L2_error = 2.626998e-05
Iteration 7: correction_norm = 8.143265e-04, L2_error = 1.230202e-09
Iteration 8: correction_norm = 3.734667e-08, L2_error = 7.046012e-15
Iteration 9: correction_norm = 5.469294e-13, L2_error = 2.797439e-16

We visualize the convergence by plotting the \(L^2\)-error and the residual norm (\(\delta u\)) across iterations

fig = plt.figure(figsize=(12, 4))

plt.subplot(121)
plt.semilogy(np.arange(i), L2_error, 'bo')
plt.grid()

plt.xlabel("Iterations")
plt.ylabel(r"$L^2$ - error")

plt.subplot(122)
plt.semilogy(np.arange(i), du_norm, 'ro')
plt.grid()

plt.xlabel("Iterations")
plt.ylabel(r"$\vert\vert \delta u\vert\vert$");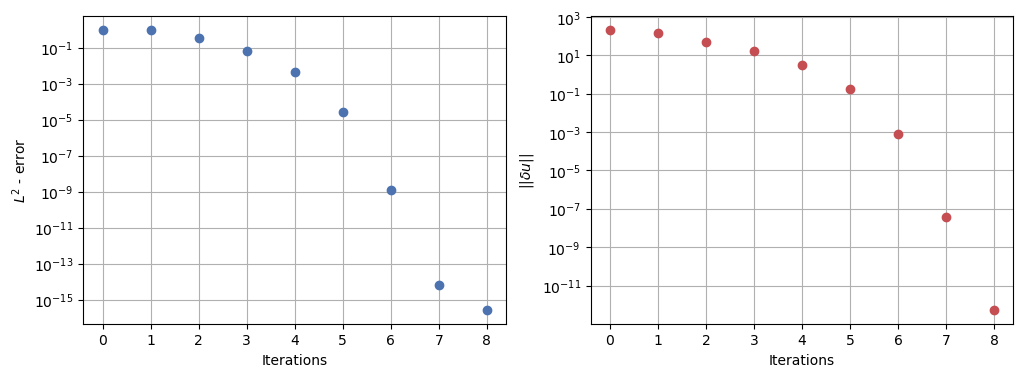

We compute the maximum error and plot the solution

error_max = domain.comm.allreduce(
  np.max(np.abs(uh.x.array -u_D.x.array)), 
  op=MPI.MAX
)

if domain.comm.rank == 0:
  print(f"Error_max = {error_max:.6e}")
Error_max = 8.881784e-16
from pathlib import Path

results_folder = Path("fenicsx/best_practices")
results_folder.mkdir(exist_ok=True, parents=True)

u_topology, u_cell_types, u_geometry = dolfinx.plot.vtk_mesh(V)
u_grid = pyvista.UnstructuredGrid(u_topology, u_cell_types, u_geometry)

u_grid.point_data["u"] = uh.x.array.real
u_grid.set_active_scalars("u")

u_plotter = pyvista.Plotter(off_screen=False)
u_plotter.add_mesh(u_grid, show_edges=True)
u_plotter.view_xy()

if not pyvista.OFF_SCREEN:
  #u_plotter.show()
  u_plotter.export_html(results_folder/"newton_solution.html")